卡尔曼滤波

更新于 分类： 阅读次数： 本文字数： 1.3k 阅读时长 ≈ 5 分钟

卡尔曼滤波（Kalman filtering）一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波过程。

I. 卡尔曼滤波器

II. 扩展卡尔曼滤波器

经典的卡尔曼滤波只适用于线性且满足高斯分布的系统，但实际工程中并不是这么简单，比如飞行器在水平运动时有可能伴随着自身的自旋，此时的系统并不是线性的，这时就需要应用扩展卡尔曼滤波（EKF）来解决这种情况1。

在扩展卡尔曼滤波器（Extended Kalman Filter，简称EKF）中状态转换和观测模型不需要是状态的线性函数，可替换为（可微的）函数。函数f可以用来从过去的估计值中计算预测的状态，相似的，函数h可以用来以预测的状态计算预测的测量值。然而f和h不能直接的应用在协方差中，取而代之的是计算偏导矩阵（Jacobian）。

\[{ {x} }_{k}=f({ {x} }_{k-1},{ {u} }_{k},{ {w} }_{k})\]

当前状态的概率分布是关于上一状态和将要执行的控制量的二元函数，再叠加一个高斯噪声，测量值同样是关于当前状态的函数叠加高斯噪声。具体表达式如下： \(g(u_t, x_{t-1})\) 和 \(h(x_t)\) 可以是非线性的函数。

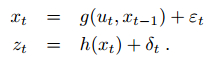
为了用经典卡尔曼滤波器的思想来解决非线性系统中的状态估计问题，首先要做的就是把 \(g(u_t, x_{t-1})\) 和 \(h(x_t)\) 用泰勒级数展开，将其线性化，只取一次项为一阶EKF滤波。具体如下：

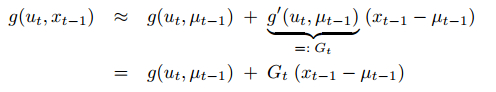
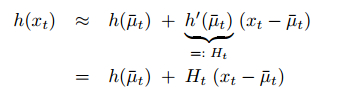
\(g(u_t, x_{t-1})\) 在上一状态估计的最优值处取一阶导数，\(h(x_t)\) 在当前时刻预测值处取一阶导数，得到G和H分别相当于Kalman Filter中的A和C。

在每一步中使用当前的估计状态计算Jacobian矩阵，这几个矩阵可以用在卡尔曼滤波器的方程中。这个过程，实质上将非线性的函数在当前估计值处线性化了。

这样一来，卡尔曼滤波器的等式为（非线性离散方程，对于非线性连续微分方程来说，需要先一阶近似离散）：

\[{\hat { {x} } }_{k|k-1}=f({ {x} }_{k-1},{ {u} }_{k},0)\]

使用Jacobians矩阵更新模型：

\[ {F}_{k}=\left.{\frac {\partial f}{\partial { {x} } } }\right\vert _{ {\hat {x} }_{k-1|k-1},{ {u} }_{k} } \]

\[ { {H} }_{k}=\left.{\frac {\partial h}{\partial { {x} } } }\right\vert _{ {\hat{x} }_{k|k-1} } \]

状态矩阵A的雅克比矩阵：

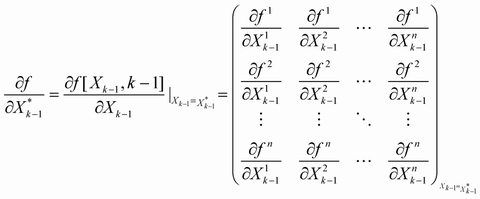
观测矩阵H的雅克比矩阵：

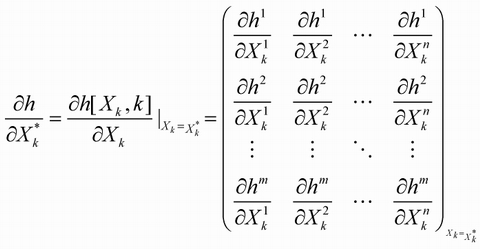
Extended Kalman Filter五条黄金公式 ：

II.I. 更新

\[{\displaystyle {\tilde { {y} } }_{k}={ {z} }_{k}-h({\hat { {x} } }_{k|k-1},0)}\]

\[{\displaystyle { {S} }_{k}={ {H} }_{k}{ {P} }_{k|k-1}{ {H} }_{k}^{T}+{ {R} }_{k} }\]

\[{\displaystyle { {K} }_{k}={ {P} }_{k|k-1}{ {H} }_{k}^{T}{ {S} }_{k}^{-1} }\]

\[{\displaystyle {\hat { {x} } }_{k|k}={\hat { {x} } }_{k|k-1}+{ {K} }_{k}{\tilde { {y} } }_{k} }\]

\[{\displaystyle { {P} }_{k|k}=(I-{ {K} }_{k}{ {H} }_{k}){ {P} }_{k|k-1} }\]

II.II. 预测

如同扩展卡尔曼滤波器（EKF）一样， UKF的预测过程可以独立于UKF的更新过程之外，与一个线性的（或者确实是扩展卡尔曼滤波器的）更新过程合并来使用；或者，UKF的预测过程与更新过程在上述中地位互换亦可。

II.III. MATLAB实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
% author :  Perry.Li  @USTC
% function: simulating the process of EKF
% date:     04/28/2015
%
N = 50;         %计算连续N个时刻
n=3;            %状态维度
q=0.1;          %过程标准差
r=0.2;          %测量标准差
Q=q^2*eye(n);   %过程方差
R=r^2;          %测量值的方差
% 离散状态方程
f=@(x)[x(2);x(3);0.05*x(1)*(x(2)+x(3))];  %状态方程
h=@(x)[x(1);x(2);x(3)];                   %测量方程
s=[0;0;1];                                %初始状态
%初始化状态
x=s+q*randn(3,1);                         
P = eye(n);                               
xV = zeros(n,N);          
sV = zeros(n,N);         
zV = zeros(n,N);
for k=1:N
  z = h(s) + r*randn;                     
  sV(:,k)= s;                             %实际状态
  zV(:,k)  = z;                           %状态测量值
  [x1,A]=jaccsd(f,x); %计算f的雅可比矩阵，其中x1对应黄金公式line2
  P=A*P*A'+Q;         %过程方差预测，对应line3
  [z1,H]=jaccsd(h,x1); %计算h的雅可比矩阵
  K=P*H'*inv(H*P*H'+R); %卡尔曼增益，对应line4
  x=x1+K*(z-z1);        %状态EKF估计值，对应line5
  P=P-K*H*P;            %EKF方差，对应line6
  xV(:,k) = x;          %save
  s = f(s) + q*randn(3,1);  %update process
end
for k=1:3
  FontSize=14;
  LineWidth=1;
  figure();
  plot(sV(k,:),'g-'); %画出真实值
  hold on;
  plot(xV(k,:),'b-','LineWidth',LineWidth) %画出最优估计值
  hold on;
  plot(zV(k,:),'k+'); %画出状态测量值
  hold on;
  legend('真实状态', 'EKF最优估计估计值','状态测量值');
  xl=xlabel('时间(分钟)');
  t=['状态 ',num2str(k)] ;
  yl=ylabel(t);
  set(xl,'fontsize',FontSize);
  set(yl,'fontsize',FontSize);
  hold off;
  set(gca,'FontSize',FontSize);
end

function [z,A]=jaccsd(fun,x)
% JACCSD Jacobian through complex step differentiation
% [z J] = jaccsd(f,x)
% z = f(x)
% J = f'(x)
%
z=fun(x);
n=numel(x);
m=numel(z);
A=zeros(m,n);
h=n*eps;
for k=1:n
    x1=x;
    x1(k)=x1(k)+h*i;
    A(:,k)=imag(fun(x1))/h;
end

  1. 扩展卡尔曼滤波器的原理及应用↩