支持向量机

更新于 2024-04-10 分类： Research 阅读次数：本文字数： 14k 阅读时长 ≈ 52 分钟

支持向量机（Support Vector Machine）是Cortes和Vapnik于1995年首先提出的，它在解决小样本、非线性及高维模式识别中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中。

最简单的SVM从线性分类器导出，根据最大化分类间隔的目标（Large Margin Classifier），我们可以得到线性可分问题的SVM训练时求解的问题（Hard SVM）。但现实应用中很多数据是线性不可分的，通过加入松弛变量和惩罚因子，可以将SVM推广到线性不可分的情况（Soft SVM）。这个优化问题是一个凸优化问题，并且满足Slater条件，因此强对偶成立，通过拉格朗日对偶可以将其转化成对偶问题求解（Dual Soft SVM）。到这里为止，支持向量机还是一个线性模型，只不过允许有错分的训练样本存在。通过核函数（Kernel Trick），可以将它转化成非线性模型，此时的对偶问题也是一个凸优化问题（Soft Kernel SVM）。这个问题的求解普遍使用的是SMO算法，这是一种分治法，它每次选择两个变量进行优化，这两个变量的优化问题是一个带等式和不等式约束条件的二次函数极值问题，可以求出公式解，并且这个问题也是凸优化问题。优化变量的选择通过KKT条件来确定。

I. 统计学习理论

支持向量机方法是建立在统计学习理论的VC 维理论和结构风险最小原理基础上的，根据有限的样本信息在模型的复杂性（即对特定训练样本的学习精度，Accuracy）和学习能力（即无错误地识别任意样本的能力）之间寻求最佳折衷，以期获得最好的推广能力（或称泛化能力）。

统计机器学习能够精确的给出学习效果，能够解答需要的样本数等等一系列问题。

VC维是对函数类的一种度量，可以简单的理解为问题的复杂程度，VC维越高，一个问题就越复杂。正是因为SVM关注的是VC维，SVM解决问题的时候，和样本的维数是无关的（甚至样本是上万维的都可以。当然，有这样的能力也因为引入了核函数）。
机器学习本质上就是一种对问题真实模型的逼近（我们选择一个我们认为比较好的近似模型，这个近似模型就叫做一个假设）。既然真实模型不知道，那么我们选择的假设与问题真实解之间究竟有多大差距（称为风险），我们就没法得知。但我们可以用某些可以掌握的量来逼近它。
- 最直观的想法就是使用分类器在样本数据上的分类的结果与真实结果之间的差值来表示，这个差值叫做经验风险\(R_{emp}(w)\)。
- 以前的机器学习方法都把经验风险最小化作为努力的目标，但回头看看经验风险最小化原则我们就会发现，此原则适用的大前提是经验风险要确实能够逼近真实风险才行。因此很多分类函数能够在样本集上轻易达到100%的正确率，在真实分类时却一塌糊涂（即所谓的推广能力差，或泛化能力差）。
- 统计学习因此而引入了泛化误差界的概念，就是指真实风险应该由两部分内容刻画，一是经验风险，代表了分类器在给定样本上的误差；二是置信风险，代表了我们在多大程度上可以信任分类器在未知文本上分类的结果。很显然，第二部分是没有办法精确计算的，因此只能给出一个估计的区间，也使得整个误差只能计算上界，而无法计算准确的值（所以叫做泛化误差界，而不叫泛化误差）。统计学习的目标从经验风险最小化变为了寻求经验风险与置信风险的和最小，即结构风险最小。SVM正是这样一种努力最小化结构风险的算法。
  - 置信风险与两个量有关，一是样本数量，显然给定的样本数量越大，我们的学习结果越有可能正确，此时置信风险越小；二是分类函数的VC维，显然VC维越大，推广能力越差，置信风险会变大。

小样本，并不是说样本的绝对数量少（实际上，对任何算法来说，更多的样本几乎总是能带来更好的效果），而是说与问题的复杂度比起来，SVM算法要求的样本数是相对比较少的。
非线性，是指SVM擅长应付样本数据线性不可分的情况，主要通过松弛变量（也有人叫惩罚变量）和核函数技术来实现，这一部分是SVM的精髓。

II. SVM

Python · SVM系列

SVM入门系列

支持向量机原理系列

Stanford机器学习---第八讲. 支持向量机SVM

解密SVM系列

【直观详解】支持向量机SVM

支持向量机SVM

【机器学习详解】SVM解二分类,多分类,及后验概率输出

用一张图理解SVM的脉络

统计学习方法– weng-JJ技术小站

支持向量机背后的数学 -对于SVM背后的数学和理论解释的快速概览及如何实现

支持向量机属于一般化线性分类器，这族分类器的特点是他们能够同时最小化经验误差与最大化几何边缘区，因此支持向量机也被称为最大边缘区分类器。除了进行线性分类之外，SVM还可以使用所谓的核技巧有效地进行非线性分类，将其输入隐式映射到高维特征空间中。

SVM本身是从感知机算法演变而来，往简单来说其实就只是改了感知机的损失函数而已，而且改完之后还很像。感知机算法是在一个线性可分的数据集中找到一个分类超平面，尽可能的将数据集划分开。

理论上这样的超平面有无数多个，但是从直觉上，我们知道离两侧数据都比较远的超平面更适合用于分类，于是我们选择了一个比较“胖”的边界的超平面作为分类界，这就是SVM。 SVM 本身“只是”一个线性模型。只有在应用了核方法后，SVM 才会“升级”成为一个非线性模型

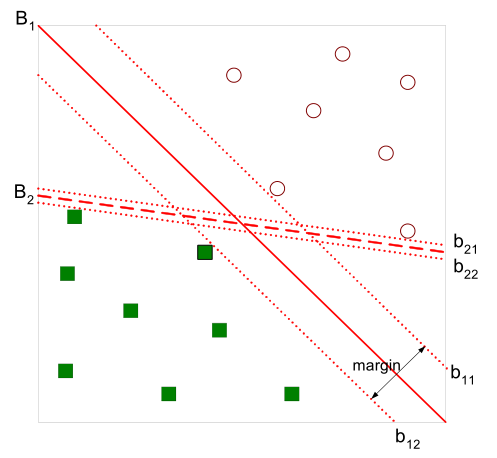
因此，支持向量机-SVM(Support Vector Machine)从本质来说是一种：用一条线（方程）分类两种事物。SVM的任务是找到这条分界线使得它到两边的margin（构成了两条平行于分离超平面的长带，二者之间的距离称之为margin）都最大。注意，这里的横坐标是 \(x_1\) 纵坐标为 \(x_2\)，如下图所示。让我们想象两个类别：红色和蓝色，我们的数据有两个特征：x 和 y。我们想要一个分类器，给定一对（x，y）坐标，输出仅限于红色或蓝色。支持向量机会接受这些数据点，并输出一个超平面（在二维的图中，就是一条线）以将两类分割开来。这条线就是判定边界：将红色和蓝色分割开。但是，最好的超平面是什么样的？对于 SVM 来说，它是最大化两个类别边距的那种方式，换句话说：超平面（在本例中是一条线）对每个类别最近的元素距离最远。

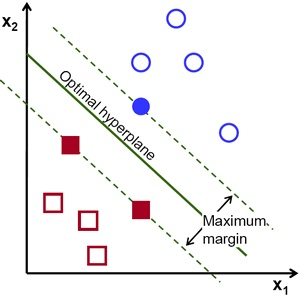
如上图所示，在Maximum Margin上的这些点就是支持向量（将距离分离超平面最近的两个不同类别的样本点称为支持向量），具体说即最终分类器表达式中只含有这些支持向量的信息，而与其他数据点无关。在下面的公式中，只有支持向量的系数 \(\alpha_i\) 不等于0。说人话，上图中两个红色的点，一个蓝色的点，合起来就是支持向量。（margin以外的样本点对于确定分离超平面没有贡献，换句话说，SVM是有很重要的训练样本（支持向量）所确定的。）

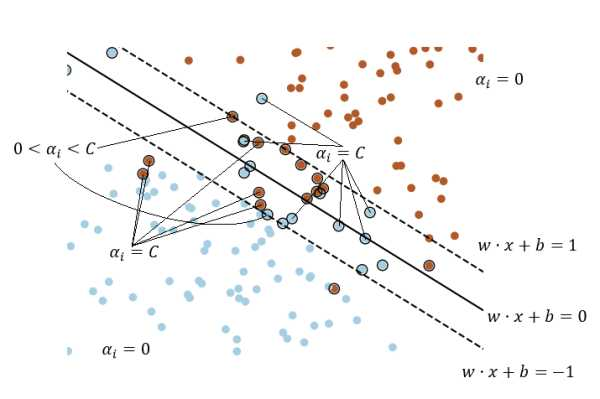
图中带黑圈的样本点即是支持向量，数学上来说的话，就是\(\alpha_i>0\)对应的样本点即是支持向量。从图中不难看出，支持向量从直观上来说，就是比较难分的样本点。此外，支持向量之所以称之为“支持”向量，是因为在理想情况下，仅利用支持向量训练出来的模型和利用所有样本训练出来的模型是一致的。这从直观上是好理解的，粗略的证明则可以利用其定义来完成：非支持向量的样本对应着\(\alpha_i=0\)，亦即它对最终模型——\(f(x)=\sum_{i=1}^N\alpha_iy_i(x_i\cdot x)+b\)没有丝毫贡献，所以可以直接扔掉。

\[ \mathbf w \cdot \varphi (\mathbf x) = \sum_i \lambda_i y_i k(\mathbf x_i,\mathbf x) \]

这里有一个视频解释可以告诉你最佳的超平面是如何找到的¹：直观可视化解释。

对于我们需要求解的这个超平面（直线）来说，我们知道它离两边一样远（待分类的两个部分的样本点），最近的距离就是到支持向量中的点的距离。根据这两点，抽象SVM的直接表达（Directly Representation）：

\[ arg \operatorname*{max}_{boundary} margin(boundary) \\ \text{所有正确归类的两类到boundary的距离} \ge margin \tag{1} \]

注：\(arg \operatorname*{max}_{x} f(x)\) 表示当 \(f(x)\) 取最大值时，x的取值。

II.I. 背景知识

假设样本为(x,y)，超平面为\(\Pi:w\cdot x+b=0\)

空间上的点：\(\vec{x^{(i)}}\in \mathbb{R}^n, i=1,2...m\)，\(m\) 指的是点的数量，\(\mathbb{R}^n\)表示的是 \(n\) 维空间
分界线：\(\vec{w^T} \cdot {\overrightarrow{x}}+b=0\)，简化为 \(w^T \cdot x+b=0\)

\[ \begin{split} w^T \cdot x+b&=0\\ \begin{bmatrix}w_1 & w_2\end{bmatrix}\cdot \begin{bmatrix}x_1\\x_2\end{bmatrix}+b&=0\\ w_1x_1+w_2x_2+b&=0\\ x_2=-\frac{w_1}{w_2}x_1&-b\quad\dots \quad (w_2\neq0) \end{split} \]

\[ \begin{split} \vec{w}\cdot\vec{k}&=w^T\cdot k\\ &=\begin{bmatrix}w_1 & w_2\end{bmatrix}\cdot \begin{bmatrix}1\\-\frac{w_1}{w_2}\end{bmatrix}\\ &=w_1-w_1\\ &=0\\ \end{split} \]

向量的形式更加简洁，特别是在高维空间的情况下，还有一个好处就是，矢量的形式下 \(w\) 刚好与分界线垂直，这个性质会在后面用到。\(w^T \cdot x+b=0\) 表示的是分界线上所有的点，当 \(w^T \cdot x+b>0\)时，表示的是分界线上方的区域，反之则是分界线下方的区域。
优化问题 \(\min_{w,b}\frac {\|w\|^2}2\)，使得\(y_i(w\cdot x_i+b)\ge1,\forall(x_i,y_i)\in D\) 的求解过程常称为硬间隔最大化，求解出来的超平面则常称为最大硬间隔分离超平面
优化问题 \(\min_{w,b}\left[\frac {\|w\|^2}2+C\sum_{i=1}^N\xi_i\right]\)，使得\(y_i(w\cdot x_i+b)\ge1-\xi_i,\forall(x_i,y_i)\in D（\xi_i\ge0）\) 的求解过程常称为软间隔最大化，求解出来的超平面则常称为最大软间隔分离超平面
若数据集线性可分，则最大硬间隔分离超平面存在且唯一
若数据集线性不可分，则最大软间隔分离超平面的解存在但不唯一，其中：法向量（w ）唯一,偏置量（b）可能不唯一

II.I.I. 函数间隔

样本到超平面的函数间隔为：\(y(w\cdot x+b)\)

由二维直线\(w^Tx+b=0\)扩展到高维被称为超平面\((w,b)\)。一个点距离超平面的远近可以表示分类预测的确信程度。在超平面\(w^Tx+b=0\)确定的情况下，\(|w^Tx+b|\)能够相对地表示点x距离超平面的远近，而且如果分类正确，则\(y^{(i)}\)与\(w^Tx+b\)的符号一致,即\(y^{(i)}(w^Tx^{(i)}+b)>0\)，同时表示分类的正确性以及确信度。

函数间隔：超平面\((w,b)\)关于样本点\((x^{(i)},y^{(i)})\)的函数间隔为

\[\hat{\gamma}^{(i)}=y^{(i)}(w^Tx^{(i)}+b)\]

定义超平面关于样本集S的函数间隔为超平面\((w,b)\)与S中所有样本点的函数间隔的最小值

\[\hat{\gamma}=min_{i=1,2,...m}\ \hat{\gamma}^{(i)}\]

定义\(\hat{\gamma}\)是为了最大化间隔，\(\hat{\gamma}\)表示关于超平面与训练集中样本的函数间隔最小值，下面只要最大化\(\hat{\gamma}\)即可。注意到函数间隔实际上并不能表示点到超平面的距离，因为当超平面\((w,b)\)参数扩大相同的倍数后，如\((2w,2b)\)，超平面的位置并没有改变，但是函数间隔也变大了相同的倍数\(2\hat{\gamma}^{(i)}\).

II.I.II. 几何间隔

我所理解的 SVM（支持向量机）

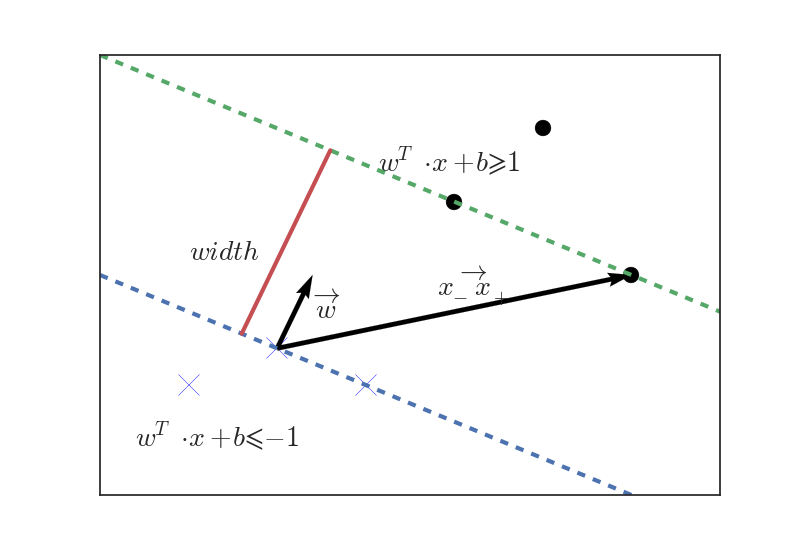
\[ \begin{split} width &=\overrightarrow{x_-x_+}\cdot \frac{\vec{w}}{||\vec{w}||}\\ &=\frac{1}{||\vec{w}||}[w^T\cdot(x_+-x_-)]\\ &=\frac{1}{||\vec{w}||}[w^T\cdot x_+-w^T\cdot x_-]\\ &=\frac{1}{||\vec{w}||}[1-b-(-1-b)]\\ &=\frac{2}{||\vec{w}||} \end{split} \]

样本到超平面的几何间隔为：\(\frac1{\|w\|}y(w\cdot x+b)\)

II.I.II.I. 解释一

设样本点A坐标为\(x^{(i)}\),点A到超平面的垂直距离记为\(\gamma^{(i)}\),分离超平面\(w^Tx^{(i)}+b=0\)的单位法向量为\(\frac{w}{||w||}\),因此点B的坐标为\(x^{(i)}-\gamma^{(i)}\frac{w}{||w||}\)，且点B在直线上，带入直线公式有：

\[w^T(x^{(i)}-\gamma^{(i)}\frac{w}{||w||})+b=0\]

\[\gamma^{(i)}=\frac{(w^Tx^{(i)}+b)}{||w||}\]

如果点被正确分类，\(y^{(i)}\)与\(\frac{(w^Tx^{(i)}+b)}{||w||}\)的符号一致，由此同理定义几何间隔

\[\gamma^{(i)}=y^{(i)}\left(\frac{w^Tx^{(i)}+b}{||w||}\right)\]

超平面与样本集S的几何间隔为

\[\gamma=min_{i=1,2,...m}\ \gamma^{(i)}\]

II.I.II.II. 解释二

我们在定义点(x,y)到平面（超平面）\(\Pi\)的间隔时，一般都是这样做的：

将\((x,y)\)（垂直）投影到\(\Pi\)上
设投影点为\((x^{\ast},y^{\ast})\)，则定义 \(d((x,y),\Pi)=\left\{ \begin{aligned} \|x-x^{\ast}\|^2,&\ \ y(w\cdot x + b) \ge0 \\ -\|x-x^{\ast}\|^2,&\ \ y(w\cdot x + b) <0 \end{aligned} \right.\).

注意这里我们允许（当样本被错分类时的）间隔为负数，所以间隔其实严格来说并不是一般意义上的距离。

那么为了找到垂直投影，我们得先找到垂直于超平面\(\Pi\)的方向。不难看出w就是垂直于\(\Pi\)的，因为对\(\forall x_1,x_2\in\Pi\)，由\(\left\{ \begin{aligned} &w\cdot x_1+b=0 \\ &w\cdot x_2+b=0 \end{aligned} \right.\)知\(w\cdot(x_1-x_2)=0\)（两式相减即可），从而w垂直于向量\(x_1-x_2\)，从而也就垂直于\(\Pi\)：

那么结合之前那张图，不难得知我们可以设\(x-x^{\ast} =\lambda w\)（这里的\(\lambda\)可正可负），于是就有（注意由\(x^{\ast} \in\Pi\)知\(w\cdot x^{\ast} +b=0\)）

\[ \begin{align} \|x-x^{\ast} \|^2&=(x-x^{\ast} )\cdot(x-x^{\ast} )=\lambda w\cdot(x-x^{\ast} ) \\ &=\lambda \left[w\cdot(x-x^{\ast} )+(b-b)\right]\\ &=\lambda\left[ w\cdot x+b - (w\cdot x^{\ast} + b)\right] \\ &=\lambda(w\cdot x+b) \end{align} \]

从而

\[ d((x,y),\Pi)=\left\{ \begin{aligned} \lambda(w\cdot x+b),&\ \ y(w\cdot x + b) \ge0 \\ -\lambda(w\cdot x+b),&\ \ y(w\cdot x + b) <0 \end{aligned} \right. \]

注意这么定义的间隔有一个大问题：当w和b同时增大k倍时，新得到的超平面\(\tilde\Pi:(kw)\cdot x+(kb)\)其实等价于原超平面\(\Pi\)：

\[ x\in\tilde\Pi\Leftrightarrow(kw)\cdot x+(kb)=0\Leftrightarrow w\cdot x+b=0\Leftrightarrow x\in\Pi \]

但此时\(d((x,y),\Pi)\)却会直接增大k倍。极端的情况就是，当w和b同时增大无穷倍时，超平面没变，间隔却也跟着增大了无穷倍，这当然是不合理的。

所以我们需要把 scale 的影响给抹去，常见的做法就是做某种意义上的归一化：

\[ d((x,y),\Pi)=\left\{ \begin{aligned} \frac1{\|w\|}|w\cdot x+b|,&\ \ y(w\cdot x + b) \ge0 \\ -\frac1{\|w\|}|w\cdot x+b|,&\ \ y(w\cdot x + b) <0 \end{aligned} \right. \]

（注意：由于 scale 的影响已被抹去，所以\(\lambda\)也就跟着被抹去了；同时由\(0\le\|x-x^{\ast} \|^2=\lambda(w\cdot x+b)\) 知，我们需要在抹去 \(\lambda\)的同时、给\(w\cdot x+b\)套一个绝对值)

不难看出上式可改写为：

\[ d((x,y),\Pi)=\frac1{\|w\|}y(w\cdot x+b) \]

这正是我们想要的结果。

II.I.III. 间隔最大化

支持向量机的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。为了间隔最大化，只需要最大化几何间隔\(\gamma\)，同时所有样本的几何间隔必须满足\(\gamma^{(i)}\geq\gamma,i=1,2,...,m\)

\[max_{w,b}\ \gamma\]

\[s.t.\ y^{(i)}\left(\frac{w^Tx^{(i)}+b}{||w||}\right)\geq\gamma\]

上述问题，可以转变为一个凸二次规划问题，这是支持向量机的一个重要属性，局部极值即为全局最值。

考虑函数间隔与几何间隔的关系：

\[max_{\gamma,w,b}\ \frac{\hat{\gamma}}{||w||}\]

\[s.t.\ y^{(i)}\left(w^Tx^{(i)}+b\right)\geq \hat{\gamma}\]

当超平面参数\((w,b)\)同时变为\((2w,2b)\)，函数间隔也会变为\(2\hat{\gamma}\),目标函数的解并不会变化。即\(\hat{\gamma}\)的取值不影响优化问题的解。因此令\(\hat{\gamma}=1\)，目标函数变为最大化\(\frac{1}{||w||}\)，即最小化\({\|w\|^2}\)，为了后面的求解方便，添加因子1/2也不影响目标函数的解；

II.I.IV. 感知机模型

感知机模型只有\(w\)和\(b\)这两个参数，它们决定了一张超平\(\Pi:w\cdot x+b=0\)。感知机最终目的是使得\(y(w\cdot x+b)>0,\forall(x,y)\in D\)，其中D是训练数据集、y只能取正负。

训练方法则是梯度下降，其中梯度公式为：

\[ \frac{\partial L}{\partial w}(x_i,y_i) = -y_ix_i、\frac{\partial L}{\partial b}(x_i,y_i)=-y_i \]

我们在实际实现时，采用了“极大梯度下降法”（亦即每次只选出使得损失函数最大的样本点来进行梯度下降）。然后有理论证明，只要数据集线性可分，这样下去就一定能收敛。

for _ in range(epoch):
    # 计算 w·x+b
    y_pred = x.dot(self._w) + self._b
    # 选出使得损失函数最大的样本
    idx = np.argmax(np.maximum(0, -y_pred * y))
    # 若该样本被正确分类，则结束训练
    if y[idx] * y_pred[idx] > 0:
        break
    # 否则，让参数沿着负梯度方向走一步
    delta = lr * y[idx]
    self._w += delta * x[idx]
    self._b += delta

II.I.V. 优化问题的等价性

为方便，称优化问题：

\[ \min_{w,b}\left[\frac {\|w\|^2}2+C\sum_{i=1}^N\xi_i\right]，使得y_i(w\cdot x_i+b)\ge1-\xi_i,\forall(x_i,y_i)\in D（\xi_i\ge0） \]

为问题一；称：

\[ \min_{w,b}{\left[\frac{\|w\|^2}2 + C\sum_{i=1}^N[1-y_i(w\cdot x_i+b)]_ +\right]} \]

为问题二，则我们需要证明问题一与问题二等价

先来看问题一怎么转为问题二。事实上不难得知：

\[ y_i(w\cdot x_i+b)\ge1-\xi_i,\forall(x_i,y_i)\in D\Rightarrow\xi_i\ge1-y_i(w\cdot x_i+b) \]

注意问题一是针对w和b进行优化的，且当w和b固定时，为使\(\frac {\|w\|^2}2+C\sum_{i=1}^N\xi_i\)最小，必有：

\(1-y_i(w\cdot x_i+b)\ge0\)时，\(\xi_i=1-y_i(w\cdot x_i+b)\)
\(1-y_i(w\cdot x_i+b)<0\)时，\(\xi_i=0\)（因为我们要求\(\xi_i\ge0\)）

亦即\(\xi_i=[1-y_i(w\cdot x_i+b)]_ +\)。此时损失函数即为\(\frac{\|w\|^2}2 + C\sum_{i=1}^N[1-y_i(w\cdot x_i+b)]_ +\)，换句话说，我们就把问题一转为了问题二。

再来看问题二怎么转为问题一。事实上，直接令\(\xi_i=[1-y_i(w\cdot x_i+b)]_ +\)，就有：

模型的损失为\(\frac {\|w\|^2}2+C\sum_{i=1}^N\xi_i\)
模型的约束为\(\xi_i\ge 1-y_i(w\cdot x_i+b)且\xi_i\ge0\)

亦即转为了问题一

II.I.VI. 带约束的二次规划求解

不妨设我们选取出来的两个参数就是\(\alpha_1\)和\(\alpha_2\)，那么问题的关键就在于如何把\(\alpha_1\)和\(\alpha_2\)相关的东西抽取出来并把其它东西扔掉。

注意到我们的对偶问题为

\[ \max_\alpha L(\alpha)=-\frac12\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j) + \sum_{i=1}^N\alpha_i\]

使得对\(i=1,...,N\)、都有\(\sum_{i=1}^N\alpha_iy_i=0、0\le\alpha_i\le C\)。

Gram 矩阵： \(G=(x_i\cdot x_j)_ {N\times N}\)

所以L就可以改写为

\[L(\alpha)=-\frac12\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jG_{ij}+\sum_{i=1}^N\alpha_i\]

把和\(\alpha_1\)、\(\alpha_2\)无关的东西扔掉之后，L可以化简为：

\[ L(\alpha)=-\frac12(G_{11}\alpha_1^2+2y_1y_2G_{12}\alpha_1\alpha_2+G_{22}\alpha_2^2)-\left(y_1\alpha_1\sum_{i=3}^Ny_i\alpha_iG_{i1}+y_2\alpha_2\sum_{i=3}^Ny_i\alpha_iG_{i2}\right)+(\alpha_1+\alpha_2) \]

约束条件则可以化简为对i=1和i=2，都有\(y_1\alpha_1+y_2\alpha_2=-\sum_{i=3}^Ny_i\alpha_i=c\)、\(0\le\alpha_i\le C\)，其中\(c\)是某个常数

而带约束的二次规划求解过程也算简单：只需先求出无约束下的最优解，然后根据约束“裁剪”该最优解即可。

无约束下的求解过程其实就是求偏导并令其为 0。以\(\alpha_1\)为例，注意到

\[ y_1\alpha_1+y_2\alpha_2=c\Rightarrow\alpha_2=\frac c{y_2}-\frac{y_1}{y_2}\alpha_1 \]

令\(c^{\ast}=\frac c{y_2}\),\(s=y_1y_2\)，则\(c^{\ast}\)亦是常数，且由于\(y_1\)、\(y_2\)都只能取正负 1，故不难发现\(\frac{y_2}{y_1}=\frac{y_1}{y_2}=s\)，从而\(\alpha_2=c^{\ast}-s\alpha_1\Rightarrow\frac{\partial\alpha_2}{\partial\alpha_1}=-s\)

于是

\[ \begin{align} \frac{\partial L}{\partial\alpha_1}=&-G_{11}\alpha_1-y_1y_2G_{12}(\alpha_2+\alpha_1\frac{\partial\alpha_2}{\partial\alpha_1})-G_{22}\alpha_2\frac{\partial\alpha_2}{\partial\alpha_1} \\ &-y_1\sum_{i=3}^Ny_i\alpha_iG_{i1}-y_2\frac{\partial\alpha_2}{\partial\alpha_1}\sum_{i=3}^Ny_i\alpha_iG_{i2}+1 \\ =&-G_{11}\alpha_1-sG_{12}(c^{\ast}-s\alpha_1-\alpha_1\cdot s)-G_{22}(c^{\ast}-s\alpha_1)\cdot(-s) \\ &-y_1\sum_{i=3}^Ny_i\alpha_iG_{i1}+sy_2\sum_{i=3}^Ny_i\alpha_iG_{i2}+\left(\frac{\partial\alpha_2}{\partial\alpha_1}+1\right) \end{align} \]

考虑到\(s^2=1\)、\(sy_2=y_1\)、Gram 矩阵是对称阵、且模型在第k个样本\(x_k\)处的输出为\(f(x_k)=\sum_{i=1}^N\alpha_iy_i(x_i\cdot x_k)+b=\sum_{i=1}^N\alpha_iy_iG_{ik}+b\)，从而可知

\[ \begin{align} \frac{\partial L}{\partial\alpha_1}=&-G_{11}\alpha_1-sG_{12}c^{\ast}+2G_{12}\alpha_1+sG_{22}c^{\ast}-G_{22}\alpha_1 \\ &-y_1[f(x_1)-y_1\alpha_1G_{11}-y_2\alpha_2G_{21}] \\ &+y_1[f(x_2)-y_1\alpha_1G_{12}-y_2\alpha_2G_{22}] +(1-s) \end{align} \]

令\(v_i=(f(x_i)-b)-y_1\alpha_1G_{1i}-y_2\alpha_2G_{2i}\ \ (i=1,2)\)，则

\[ \frac{\partial L}{\partial\alpha_1}=-(G_{11}-2G_{12}+G_{22})\alpha_1-sc^{\ast}(G_{12}-G_{22})-y_1(v_1-v_2)+(1-s) \]

于是

\[ \begin{align} \frac{\partial L}{\partial\alpha_1}=0\Rightarrow\alpha_1&=-\frac{sc^{\ast}(G_{12}-G_{22})+y_1(v_1-v_2)-(1-s)}{G_{11}-2G_{12}+G_{22}} \\ &=-\frac{y_1[y_2c^{\ast}(G_{12}-G_{22})+(v_1-v_2)-(y_1-y_2)]}{G_{11}-2G_{12}+G_{22}} \end{align} \]

注意到\(c^{\ast}=s\alpha_1+\alpha_2\)，从而

\[ y_2c^{\ast}(G_{12}-G_{22})=y_2(s\alpha_1+\alpha_2)(G_{12}-G_{22})=(y_1\alpha_1+y_2\alpha_2)(G_{12}-G_{22}) \]

令\(dG=G_{11}-2G_{12}+G_{22}、e_i=f(x_i)-y_i\ \ (i=1,2)\)，则

\[ y_2c^{\ast}(G_{12}-G_{22})+(v_1-v_2)-(y_2+y_1)=... =e_1 - e_2 - y_1\alpha_1dG \]

从而

\[ \alpha_1^{new,raw}=\alpha_1^{old}-\frac{y_1(e_1-e_2)}{dG} \]

接下来就要对其进行裁剪了。注意到我们的约束为\(0\le\alpha_i\le C\)、\(\alpha_1y_1+\alpha_2y_2\)为常数，所以我们需要分情况讨论\(\alpha_1\)的下、上界。

当\(y_1\),\(y_2\)异号（\(y_1y_2=-1\)）时，可知\(\alpha_1-\alpha_2\)为常数、亦即 \(\alpha_1^{new}-\alpha_2^{new}=\alpha_1^{old}-\alpha_2^{old}\Rightarrow\alpha_2^{new}=\alpha_1^{new}-(\alpha_1^{old}-\alpha_2^{old})\)，结合\(0\le\alpha_2\le C\)，可知：
- \(\alpha_1^{new}\)不应小于\(\alpha_1^{old}-\alpha_2^{old}\)，否则\(\alpha_2\)将小于 0
- \(\alpha_1^{new}\)不应大于\(C+\alpha_1^{old}-\alpha_2^{old}\)，否则\(\alpha_2\)将大于 \(C\)
当\(y_1\),\(y_2\)同号（\(y_1y_2=1\)）时，可知\(\alpha_1+\alpha_2\)为常数、亦即 \(\alpha_1^{new}+\alpha_2^{new}=\alpha_1^{old}+\alpha_2^{old}\Rightarrow\alpha_2^{new}=(\alpha_1^{old}+\alpha_2^{old}) - \alpha_1^{new}\)，结合\(0\le\alpha_2\le C\)，可知：
- \(\alpha_1^{new}\)不应小于\(\alpha_1^{old}+\alpha_2^{old}-C\)，否则\(\alpha_2\)将大于 \(C\)
- \(\alpha_1^{new}\)不应大于\(\alpha_1^{old}+\alpha_2^{old}\)，否则\(\alpha_2\)将小于 0

综上可知

\(\alpha_1^{new}\)的下界为\(U=\left\{\begin{aligned} \max\{0,\alpha_1^{old}-\alpha_2^{old}\}\ \ &y_1y_2=-1 \\ \max\{0,\alpha_1^{old}+\alpha_2^{old}-C\}\ \ &y_1y_2=1 \end{aligned} \right.\)
\(\alpha_1^{new}\)的上界为\(V=\left\{\begin{aligned} \min\{C,C+\alpha_1^{old}-\alpha_2^{old}\}\ \ &y_1y_2=-1 \\ \max\{C,\alpha_1^{old}+\alpha_2^{old}\}\ \ &y_1y_2=1 \end{aligned} \right.\)

那么直接做一个 clip 即可得到更新后的\(\alpha_1\)：

1	alpha1_new = np.clip(alpha1_new_raw, u, v)

注意由于我们要保持\(\alpha_1y_1+\alpha_2y_2\)为常数，所以（注意\(\frac{y_1}{y_2}=y_1y_2\)）

\[ \begin{align} \alpha_2^{new}&=\frac1{y_2}(\alpha_1^{old}y_1+\alpha_2^{old}y_2-\alpha_1^{new}y_1) \\ &=\alpha_2^{old}+y_1y_2(\alpha_1^{old}-\alpha_1^{new}) \end{align} \]

综上所述，我们就完成了一次参数的更新，之后就不断地更新直至满足停机条件即可

II.II. Hard Linear SVM

注意我们感知机的损失函数为 \(\sum_{i=1}^N[-y(w\cdot x+b)]_ +\)。由感知机损失函数的形式可知，感知机只要求样本被正确分类，而不要求样本被“很好地正确分类”。这就导致感知机弄出来的超平面（通常又称“决策面”）经常会“看上去很不舒服”。

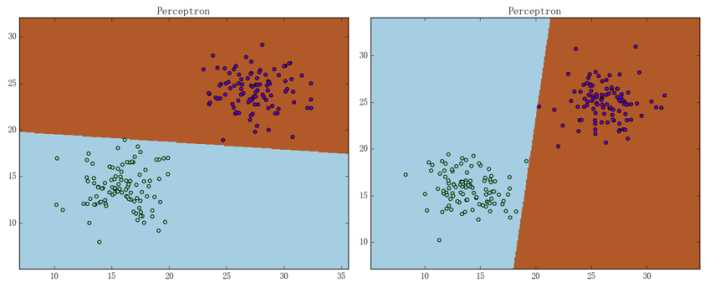
从直观上来说，我们希望得到的是这样的决策面：

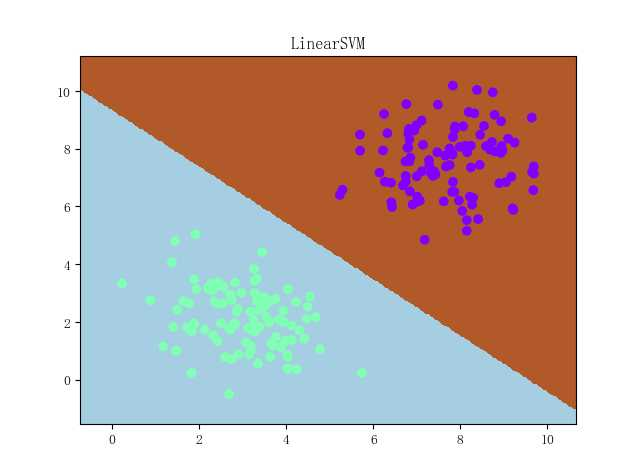
那么应该如何将这种理想的决策面的状态翻译成机器能够学习的东西呢？直观来说，就是让决策面离正负样本点的间隔都尽可能大。

首先定义超平面：\(\mathbf w^T \vec x_i + b = 0\)（w是这个超平面的法向量），接下来为了方便，设 \(\vec x = (x_1,x_2)\) 即一条直线。任意点 \(\vec x_i\) 到该直线的距离为 \(d=\frac{1}{\lVert \mathbf w \lVert} |\mathbf w^T \vec x_i + b|\) （解析几何的知识）。对于空间内所有训练点的坐标记为 \((\vec x_i,y_i)\)，其中 \(y_i\) = 1 or -1，表示点 \(\vec x_i\) 所属的类。绝对值符号会导致函数不平滑，又因为数据集是线性可分的，所以我们可以把距离公式改写为：\(d=\frac{1}{\lVert \mathbf w \lVert} y_i (\mathbf w^T \vec x_i + b)\)。

因此，这个“间隔”翻译成数学语言，其实就是简单的：

\[ d((x,y),\Pi)=\frac {1}{\|w\|}y(w\cdot x+b) \]

在有了样本点到决策面的间隔后，数据集到决策面的间隔也就好定义了：

\[ d(D, \Pi)=\min_{(x,y)\in D}d((x,y),\Pi) \]

如果这些训练数据是线性可分的，也可称为硬间隔（Hard Margin）。选出两条直线（图中的虚线），使得他们的距离尽可能的大，这两条直线的中央就是待求的超平面（直线）。为了表达直观，我们定义这两个超平面（直线）分别为 \(\mathbf w^T \vec x_i + b = 1\) 和 \(\mathbf w^T \vec x_i + b = -1\)，两个超平面（直线）之间的距离为 \(\gamma = \frac{2}{\lVert \mathbf w \lVert}\) 。

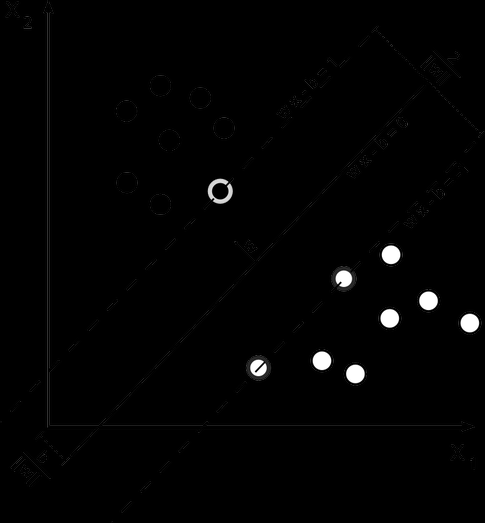
为了使得所有样本数据都在间隔区（两条虚线）以外，我们需要保证对于所有的 \(i\) 满足下列的条件: \(\mathbf w^T \vec x_i + b \geqslant 1\) 若 \(y_i = 1\)，\(\mathbf w^T \vec x_i + b \leqslant -1\) 若 \(y_i = -1\) 。上述两个条件可以写作 \(y_i(\mathbf w^T \vec x_i + b) \geqslant 1, \quad\text{for all}\quad 1\leqslant i \leqslant n\) ，这里的n指样本点的数量。

上面的表达（Directly Representation）可以被写成：让所有样本点都被正确分类：\(y(w\cdot x+b)>0,\forall(x,y)\in D\) 让决策面离正负样本点的间隔都尽可能大，最终目的是找到具有“最大间隔”（Maximum Margin）的划分超平面（直线），找到参数 \(\mathbf w\) 和 \(b\) 使得 \(d\) 最大。

\[ margin(b,w)=min_{w,b} \quad d \tag{2}\]

\[ arg \operatorname*{max}_{\mathbf w,b} \left\{ {\frac{1}{\lVert \mathbf w \lVert} \operatorname*{min}_{n} [y_i(\mathbf w^T\vec x_i}+b)]\right\} \tag{3} \]

\[ \max\min_{(x,y)\in D}\frac {1}{\|w\|}y(w\cdot x+b) \]

注意到\(y(w\cdot x+b)>0\)的性质和\(\frac {1}{\|w\|}y(w\cdot x+b)\)的值在w和b同时扩大 k 倍时不会改变。

我们知道同时放缩一个超平面的系数并不会改变这个超平面，such as 3wx+3b=0=wx+b，所以我们可以假设离我们超平面最近的那个向量到平面的距离为1。选择1的好处是，w和b进行尺缩变换（kw和kb）不改变距离，方便计算。

所以我们完全可以假设：若 \((x^{\ast},y^{\ast})=\arg\min_{(x,y)\in D}\frac {1}{\|w\|}y(w\cdot x+b)\)，则\(y^{\ast}(w\cdot x^{\ast}+b)=1\) （否则假设\(y^{\ast}(w\cdot x^{\ast}+b)=c\)，令\(w\leftarrow\frac wc\),\(b\leftarrow\frac bc\)即可）。

注意由于\((x^{\ast},y^{\ast})=\arg\min_{(x,y)\in D}\frac {1}{\|w\|}y(w\cdot x+b)\)这个最小化过程中\(w\)是固定的，所以我们可以把\(\frac1{\|w\|}\)这一项拿掉，从而：

\[ (x^{\ast},y^{\ast})=\arg\min_{(x,y)\in D}y(w\cdot x+b) \]

所以\(y^{\ast}(w\cdot x^{\ast}+b)=1\Rightarrow y(w\cdot x+b)\ge1,\forall(x,y)\in D\)

则可以对\((3)\)式进行形式变换，得到 canonical representation（最大化问题不是很好解决，我们可以转换为我们熟悉最小化问题）：

\[ \max_{w,b}\frac {1}{\|w\|}，使得y_i(w\cdot x_i+b)\ge1,\forall(x_i,y_i)\in D \]

\[ \min_{w,b}\frac {\|w\|^2}2，使得y_i(w\cdot x_i+b)\ge1,\forall(x_i,y_i)\in D \]

\[ arg \operatorname*{max}_{\mathbf w,b} \frac{2}{\lVert \mathbf w \lVert} \implies arg \operatorname*{min}_{\mathbf w,b} \frac{1}{2}\lVert \mathbf w \lVert ^2 \\ s.t.\quad y_i(\mathbf w^T\vec x_i+b) \geqslant1,\quad i = 1,2,\ldots,m \tag{4} \]

注：s.t.：subject to 表示约束条件，表达的意思等价于：为了使得所有样本数据都在间隔区（两条虚线）以外。

但是这会导致另一个问题：当数据集线性不可分时，上述优化问题是必定无解的，这就会导致模型震荡（换句话说，\(y_i(w\cdot x_i+b)\ge1\)这个约束太“硬”了）。

II.III. Dual Linear SVM

为什么我们还要考虑它的对偶问题？这是因为化作对偶问题后会更容易求解，同样也方便引入Kernel Trick。表现在 SMO 上的话就是，我们可以通过简单粗暴地将核矩阵K代替 Gram 矩阵G来完成核方法的应用。直观地说，我们只需将上面所有出现过的\(G\)都换成\(K\)就行了。

为了解\((4)\)式，需要用到拉格朗日乘子法（Method of lagrange multiplier），它是用来求解在约束条件目标函数的极值的。）

根据约束的形式，我们引入m个拉格朗日乗法子，记为 \(\boldsymbol \lambda = (\lambda_1,\ldots,\lambda_m)^T\) ，原因是，有m个约束，所以需要m个拉格朗日乗法子。可以得出拉格朗日方程如下：

\[ \mathcal{L}(\mathbf w,b,\boldsymbol \lambda) = \frac{1}{2}\lVert \mathbf w \lVert ^2 - \sum_{i=1}^m \lambda_i \{ y_i(\mathbf w^T\vec x_i+b) -1 \} \tag{5} \]

根据拉格朗日对偶性，原始的约束最优化问题可等价于极大极小的对偶问题：

\[ \max_{\alpha} \min_{w,b} \quad \mathcal{L}(w,b,\lambda) \]

解这个拉格朗日方程，对 \(\mathbf w\) 和 \(b\) 求偏导数并令其等于0，可以得到以下两个条件

\[ \mathbf w = \sum_{i=1}^m \lambda_i y_i \vec x_i \\ 0 = \sum_{i=1}^m \lambda_i y_i \]

将这两个条件带回公式(4)，可以得到对偶形式（dual representaiton），我们的目的也变为最大化 \(\mathcal{L}(\boldsymbol \lambda)\)，表达式如下:

\[ arg \operatorname*{max}_{\boldsymbol \lambda}\mathcal{L}(\boldsymbol \lambda) = \sum_{i=1}^m \lambda_i - \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \lambda_i \lambda_j \vec x_i \vec x_j \mathbf x_i^T \mathbf x_j \\ s.t. \quad \lambda_i \geqslant 0, \forall i;\quad \sum_{i=1}^m \lambda_i y_i = 0 \tag{6} \]

等价于最优化问题：

\[ \begin{align} \min_{\alpha} \quad \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j (x_i \cdot x_j) - \sum_{i=1}^{N}\alpha_i \\ s.t. \quad \sum_{i=1}^{N}\alpha_i y_i = 0 ; \alpha_i \ge 0, \quad i=1,2,\cdots,N \end{align} \]

以上表达式可以通过二次规划算法解出 \(\boldsymbol \lambda\) 后，带回，求出\(\mathbf w\) 和 \(b\)，即可得到模型：

\[ f(\mathbf x) = \mathbf w^T\mathbf x + b = \sum_{i=1}^m \lambda_i y_i \mathbf x_i^T \mathbf x + b \tag{7} \]

这显然又是一个二次规划问题！所\((4)\)式的约束是一个不等式约束，所以我们可以使用KKT条件得到三个条件：

\[ \lambda_i \geqslant0 ;\quad y_i f(\mathbf x_i)-1 \geqslant0; \quad \lambda_i\{ y_i f(\mathbf x_i)-1 \}=0 \]

使用这些条件，可以构建高效算法来解这个方程，比如SMO（Sequential Minimal Optimization）就是其中一个比较著名的，这就是对偶问题的求解方案。至于SMO是如何做的，考虑到现代很多SVM的Pakage都是直接拿来用，秉承着前人付出了努力造了轮子就不重复造的核心精神，直接调用就好。

II.IV. Soft Linear SVM

上面的例子很简单，因为那些数据是线性可分的——我们可以通过画一条直线来简单地分割红色和蓝色。然而，大多数情况下事情没有那么简单。如果样本数据你中有我我中有你（线性不可分），应该如何处理呢？你无法找出一个线性决策边界（一条直线分开两个类别）。这里就需要引入软间隔（Soft Margin），意味着，允许支持向量机在一定程度上出错。

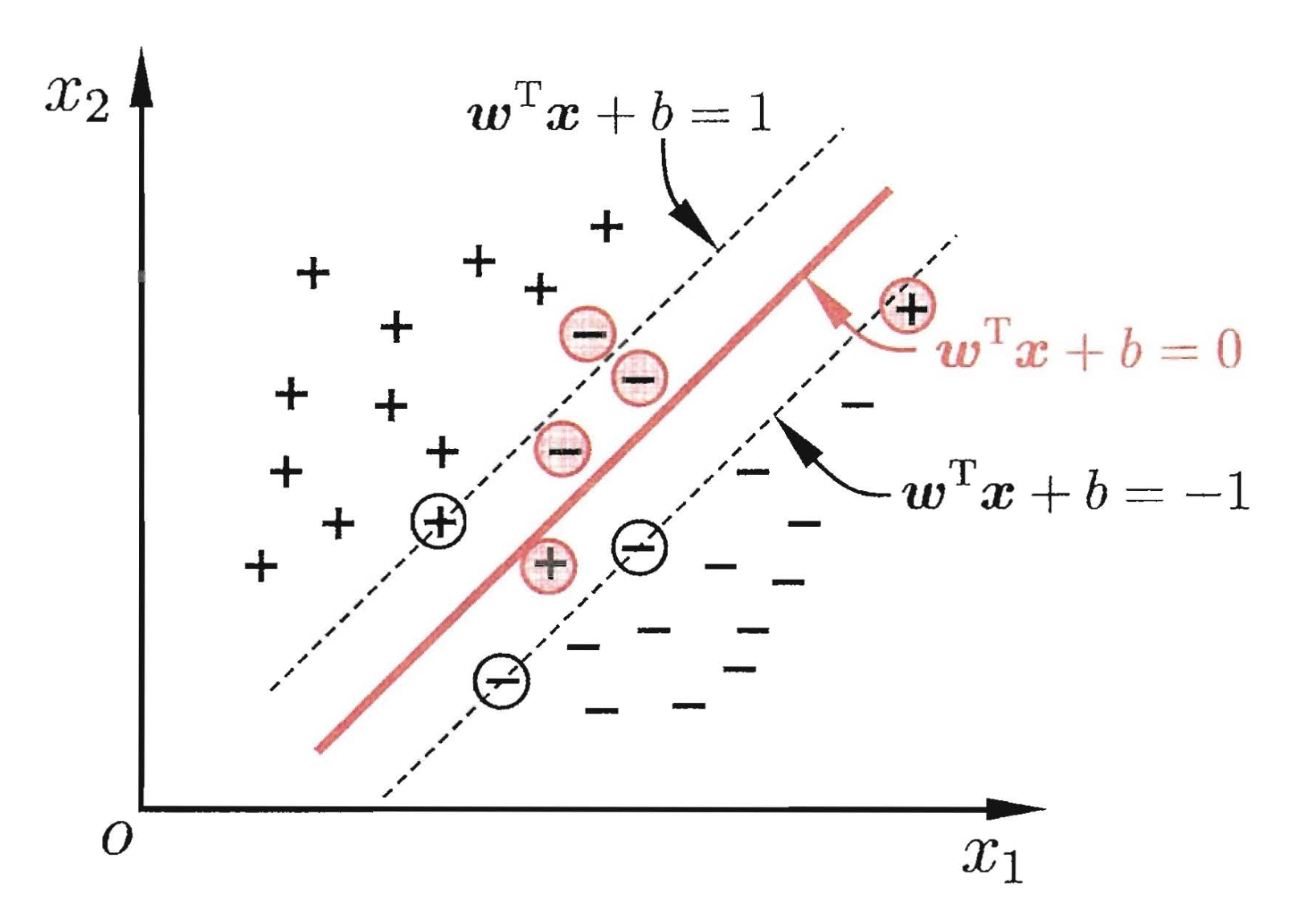
由上一节我们得知，约束为： \(y_i(\mathbf w^T\vec x_i+b) \geqslant1,\quad i = 1,2,\ldots,m\) ，目标是使目标函数可以在一定程度不满足这个约束条件，我们引入常数 \(C\) 和损失函数 \(\ell_{0/1}(z)\) 为0/1损失函数，当z小于0函数值为1，否则函数值为0。

\[ \operatorname*{min}_{\mathbf w,b} \frac{1}{2}\lVert w \lVert^2 + C \sum_{i=1}^m \ell_{0/1}(y_i(\mathbf w^T\vec x_i+b) -1) \tag {8} \]

对于\((8)\)式来说 \(C \geqslant 0\) 是个常数，当C无穷大时，迫使所有样本均满足约束；当C取有限值时，允许一些样本不满足约束。但 \(\ell_{0/1}(z)\) 损失函数非凸、非连续，数学性质不好，不易直接求解，我们用其他一些函数来代替它，叫做替代损失函数（surrogate loss）。

\[ \begin{align} & \text{hinge损失:} \ell_{hinge}(z) = max(0,1-z)\\ & \text{指数损失:} \ell_{exp}(z) = e^{-z}\\ & \text{对数损失:} \ell_{log}(z) = log(1+e^{-z})\\ \end{align} \]

三种常见损失函数如下图：

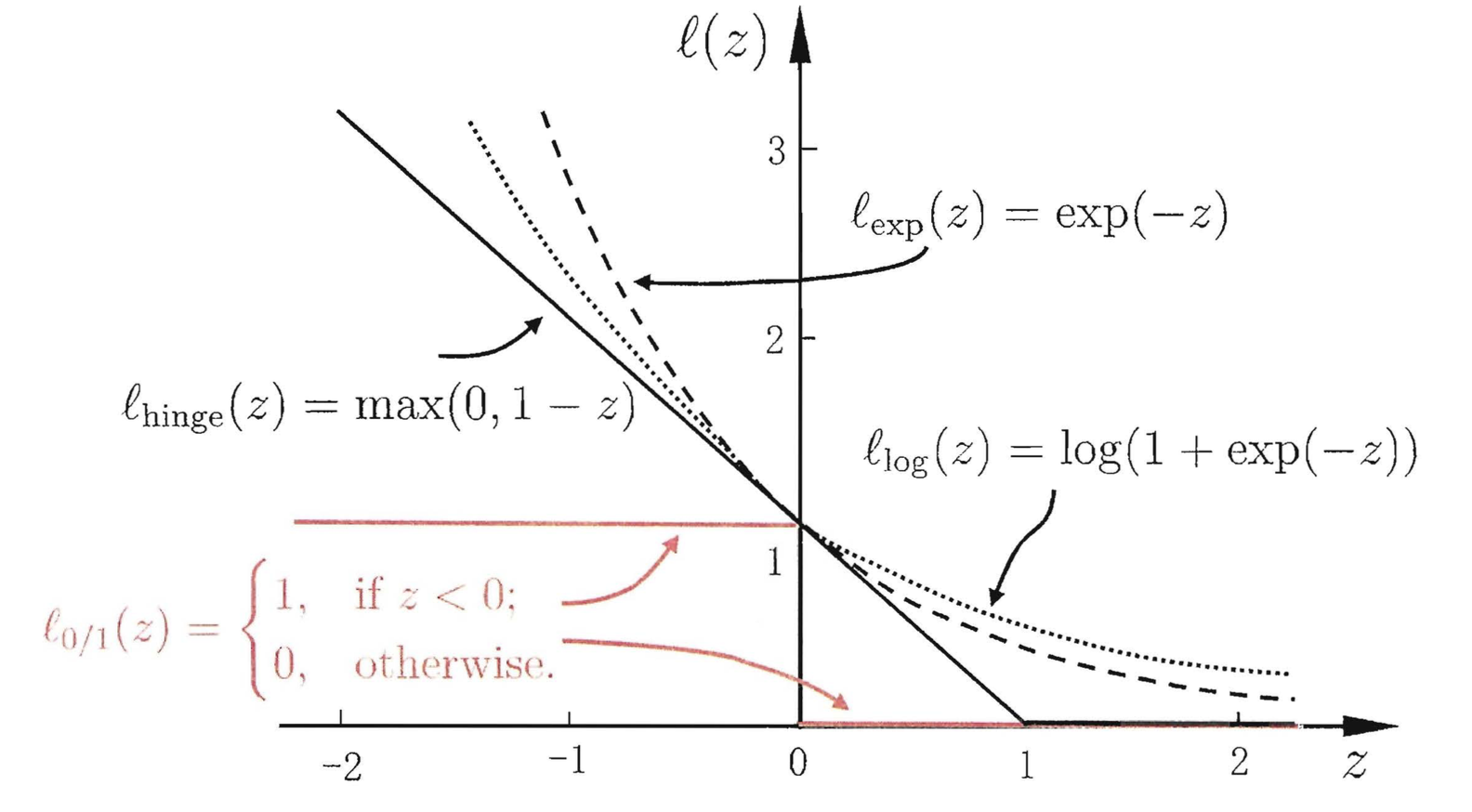
我们已知Hard LinearSVM 问题为

\[ \min_{w,b}\frac {\|w\|^2}2，使得y_i(w\cdot x_i+b)\ge1,\forall(x_i,y_i)\in D \]

且式中的\(y_i(w\cdot x_i+b)\)其实就是（没有抹去 scale 的影响的）间隔。所以想要放松对模型的限制的话，很自然的想法就是让这个间隔不必一定要不小于 1、而是只要不小于\(1-\xi_i\)就行，其中\(\xi_i\)是个不小于 0 的数。

所以为了让模型在线性不可分的数据上仍有不错的表现，从直观来说，我们应该“放松”对我们模型的限制（让我们模型的约束“软”一点），引入松弛变量（slack variables） ：

\[ \min_{w,b}\frac {\|w\|^2}2，使得y_i(w\cdot x_i+b)\ge1-\xi_i,\forall(x_i,y_i)\in D, \xi_i \ge 0 \]

正如前文所说，只放松限制的话肯定不行，会使模型变得怠惰，还得给这个放松一些惩罚。若假设数据集为\(D=\left\{(x_1,y_1),...,(x_N,y_N)\right\}\)的话，那么经过数学变换后，可将\((8)\)式重写为：

\[ \min_{w,b}{\left[\frac{\|w\|^2}2 + C\sum_{i=1}^N[1-y_i(w\cdot x_i+b)]_ +\right]} \]

其中 “\([ \cdot ]_ +\)”其实就是 ReLU 函数。于是可以看出，SVM 在形式上和感知机的差别只在于损失函数，且这两个损失函数确实长得很像。

\[ [x]_ +=\left\{ \begin{aligned} 0&\ \ x\le0 \\ x&\ \ x>0 \end{aligned} \right. \]

综上所述，在目标优化函数中加一个\(C\xi_i\)，其中\(C\)是个大于 0 的常数，可以理解为对放松的惩罚力度。优化问题即可合理地转化为：

\[ \min_{w,b}\left[\frac {\|w\|^2}2+C\sum_{i=1}^N\xi_i\right]，使得y_i(w\cdot x_i+b)\ge1-\xi_i,\forall(x_i,y_i)\in D（\xi_i\ge0） \]

\[ \operatorname*{min}_{\mathbf w,b,\xi_i} \frac{1}{2}\lVert w \lVert^2 + C \sum_{i=1}^m \xi_i \\ s.t. \quad y_i(\mathbf w^T\vec x_i+b) \geqslant 1 - \xi_i ;\quad \xi_i \geqslant 0,\quad i = 1,2,\ldots,m \tag{9} \]

\((9)\)式就是常见的软间隔支持向量机，其中，每一个样本都有一个对应的松弛变量，用以表征该样本不满足约束的程度。\(C\)为惩罚函数，目标函数有两层含义：margin尽量大，误分类的样本点计量少。

不难得知原始问题相应的拉格朗日函数为：

\[ L=\frac{\|w\|^2}2+C\sum_{i=1}^N\xi_i-\sum_{i=1}^N\alpha_i[y_i(w\cdot x_i+b)-1+\xi_i]-\sum_{i=1}^N\beta_i\xi_i \]

其中\(\alpha_i\ge0、\beta_i\ge0\)，

于是 KKT 条件的其中四个约束即为（不妨设最优解为\(w^{\ast}\)、\(b^{\ast}\)、\(\xi^{\ast}\)、\(\alpha^{\ast}\)和\(\beta^{\ast}\)）：

\(\alpha_i^{\ast}\ge0\),\(\beta_i^{\ast}\ge0\)（这是拉格朗日乘子法自身的要求）
\(\xi_i^{\ast}\ge0\)、\(y_i(w^{\ast}\cdot x_i+b^{\ast})-1+\xi_i^{\ast}\ge0\)（此即原始约束）
\(\alpha_i^{\ast}[y_i(w^{\ast}\cdot x_i+b^{\ast})-1+\xi_i^{\ast}]=0\)（换句话说，\(\alpha_i^{\ast}\)和\(y_i(w^{\ast}\cdot x_i+b)-1+\xi_i^{\ast}\)中必有一个为 0）
该等式有着很好的直观：设想它们同时不为 0，则必有\(y_i(w^{\ast}\cdot x_i+b)-1+\xi_i^{\ast}>0\)（注意原始约束）、从而\(\alpha_i^{\ast}[y_i(w^{\ast}\cdot x_i+b^{\ast})-1+\xi_i^{\ast}]\ge0\)，等号当且仅当\(\alpha_i=0\)时取得。然而由于\(\alpha_i^{\ast}\ne0\)，所以若将\(\alpha_i\)取为 0、则上述L将会变大。换句话说，将参数\(\alpha_i\)取为 0 将会使得目标函数比参数取\(\alpha_i^{\ast}\)时的目标函数要大，这与\(\alpha_i^{\ast}\)的最优性矛盾
\(\beta_i^{\ast}\xi_i^{\ast}=0（\)换句话说，\(\beta_i^{\ast}\)和\(\xi_i^{\ast}\)中必有一个为 0，理由同上）

对偶问题的实质，其实就是将原始问题

\[ \min_{w,b,\xi}\max_{\alpha,\beta} L \]

转化为对偶问题

\[ \max_{\alpha,\beta}\min_{w,b,\xi}L \]

于是我们需要求偏导并令它们为 0：

对\(w\)求偏导：\(\frac{\partial L}{\partial w}=w-\sum_{i=1}^N\alpha_iy_ix_i=0\Rightarrow w=\sum_{i=1}^N\alpha_iy_ix_i\)
对\(b\)求偏导：\(\frac{\partial L}{\partial b}=-\sum_{i=1}^N\alpha_iy_i=0\Rightarrow\sum_{i=1}^N\alpha_iy_i=0\)
对\(\xi_i\)求偏导：\(\frac{\partial L}{\partial\xi_i}=C-\alpha_i-\beta_i=0\Rightarrow\alpha_i+\beta_i=C\)

后一个 KKT 条件：最优解自然需要满足这么个条件：

\[\nabla_wL(w^{\ast},b^{\ast},\xi^{\ast},\alpha^{\ast},\beta^{\ast})=\nabla_bL(w^{\ast},b^{\ast},\xi^{\ast},\alpha^{\ast},\beta^{\ast})=\\ \nabla_\xi L(w^{\ast},b^{\ast},\xi^{\ast},\alpha^{\ast},\beta^{\ast})=0\]

注意这些约束中\(\beta_i\)除了\(\beta_i\ge0\)之外没有其它约束，\(\alpha_i+\beta_i=C\)的约束可以转为\(\alpha_i\le C\)。然后把这些东西代入拉格朗日函数L、即可得到：

\[ \begin{align} L&=\frac{\|\sum_{i=1}^N\alpha_iy_ix_i\|^2}2+\sum_{i=1}^N(C-\alpha_i-\beta_i)\xi_i-\sum_{i=1}^N\alpha_iy_i\left(\sum_{j=1}^N\alpha_jy_jx_j\right)\cdot x_i\\ -b\sum_{i=1}^N\alpha_iy_i+\sum_{i=1}^N\alpha_i \\ &=-\frac12\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum_{i=1}^N\alpha_i \end{align} \]

于是对偶问题为

\[ \max_{\alpha}\left[ -\frac12\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum_{i=1}^N\alpha_i\right]，使得\sum_{i=1}^N\alpha_iy_i=0、0\le\alpha_i\le C \]

亦即

\[ \min_{\alpha}\left[ \frac12\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum_{i=1}^N\alpha_i\right]，使得\sum_{i=1}^N\alpha_iy_i=0、0\le\alpha_i\le C \]

可以看到在对偶形式中，样本仅以内积的形式\(（x_i\cdot x_j）\)出现，这就使得核方法的引入变得简单而自然。

通过构造拉格朗日函数并求解偏导可得到等价的对偶问题：

\[ \begin{align} \min_{\alpha} \quad \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j (x_i \cdot x_j) - \sum_{i=1}^{N} {\alpha_i}\\ s.t. \quad \sum_{i=1}^{N}\alpha_i y_i = 0 ; \quad 0 \le \alpha_i \le C, \quad i=1,2,\cdots,N \end{align} \]

II.V. Soft Linear SVM的训练

虽然比较简单，但是调优 LinearSVM 的训练这个过程是相当有启发性的事情。关于各种梯度下降算法的定义、性质等等可以参见参数的更新。

II.V.I. 极大梯度下降法

极大梯度下降法其实就是随机梯度下降SGD 的特殊形式。

我们已知：

\[ L(D)=\frac{\|w\|^2}2 + C\sum_{i=1}^N[1-y_i(w\cdot x_i+b)]_ + \]

所以我们可以认为：

\[ L(x,y)=\frac{\|w\|^2}2+C[1-y(w\cdot x+b)]_ + \]

于是：

当\(y(w\cdot x+b)\ge1\)时：\(\frac{\partial L(x,y)}{\partial w} = w\)、\(\frac{\partial L(x,y)}{\partial b}=0\)
当\(y(w\cdot x+b)<1\)时：\(\frac{\partial L(x,y)}{\partial w} = w-Cyx\)、\(\frac{\partial L(x,y)}{\partial b}=-Cy\)

所以我们可以把极大梯度下降的形式写成（假设学习速率为\(\eta\)）：

\[w\leftarrow (1-\eta)w\]

若\(y(w\cdot x+b)<1\)，则选出某个被错分的样本(x,y)，然后：

\[w\leftarrow w+\eta Cyx\]

\[b\leftarrow b+\eta Cy\]

import numpy as np

class LinearSVM:
    def __init__(self):
        self._w = self._b = None

    def fit(self, x, y, c=1, lr=0.01, epoch=10000):
        x, y = np.asarray(x, np.float32), np.asarray(y, np.float32)
        self._w = np.zeros(x.shape[1])
        self._b = 0.
        for _ in range(epoch):
            self._w *= 1 - lr
            err = 1 - y * self.predict(x, True)
            idx = np.argmax(err)
            # 注意即使所有 x, y 都满足 w·x + b >= 1
            # 由于损失里面有一个 w 的模长平方
            # 所以仍然不能终止训练，只能截断当前的梯度下降
            if err[idx] <= 0:
                continue
            delta = lr * c * y[idx]
            self._w += delta * x[idx]
            self._b += delta

    def predict(self, x, raw=False):
        x = np.asarray(x, np.float32)
        y_pred = x.dot(self._w) + self._b
        if raw:
            return y_pred
        return np.sign(y_pred).astype(np.float32)

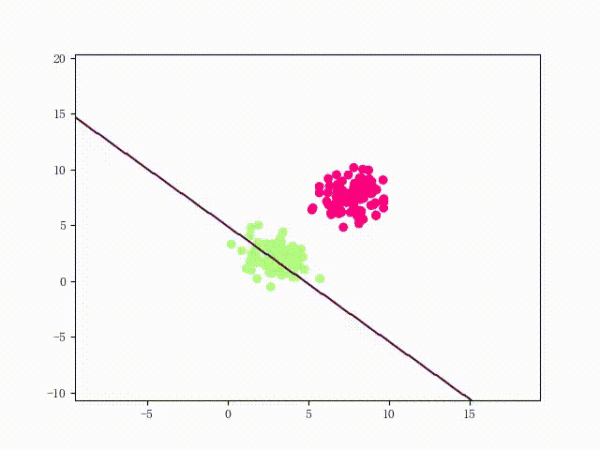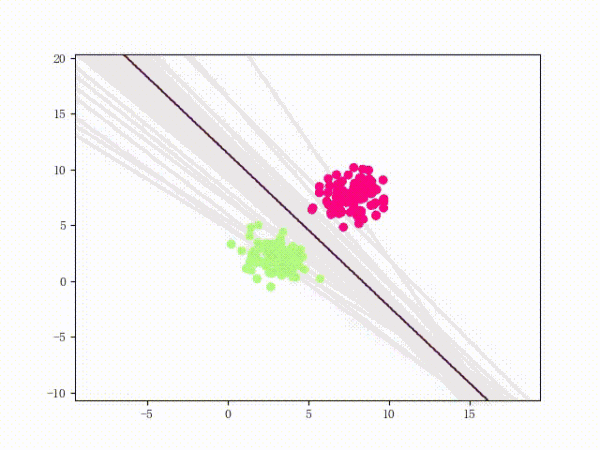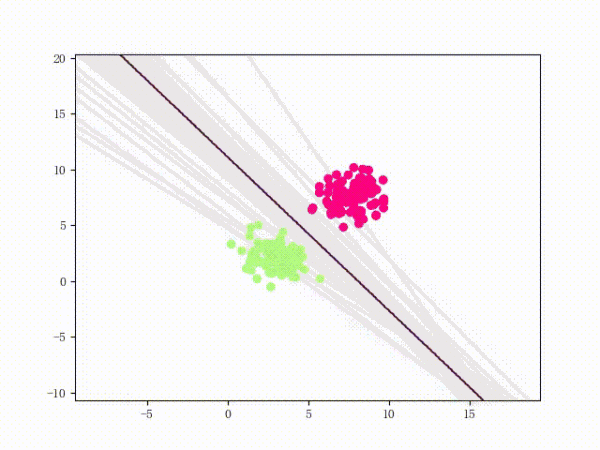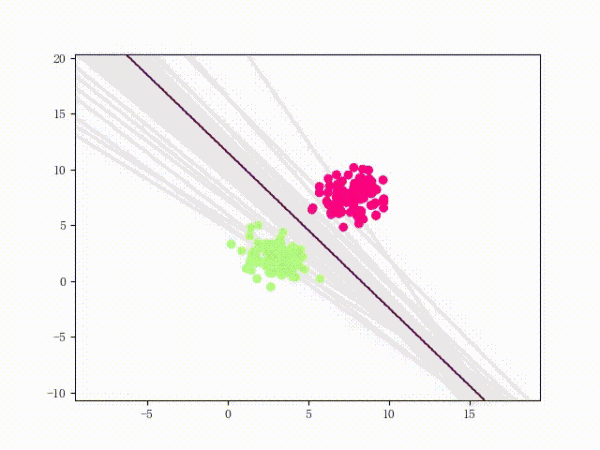
虽然看上去不错，但仍然存在着问题：

训练过程其实非常不稳定
从直观上来说，由于 LinearSVM 的损失函数比感知机要更复杂，所以相应的函数形状也会更复杂。这意味着当数据集稍微差一点的时候，直接单纯地应用极大梯度下降法可能会导致一些问题——比如说模型会卡在某个很奇怪的地方无法自拔。解释1：每次只取使得损失函数极大的一个样本进行梯度下降

通过将正负样本点的“中心”从原点 (0, 0)（默认值）挪到 (5, 5)（亦即破坏了一定的对称性）并将正负样本点之间的距离拉近一点，我们可以复现这个问题：

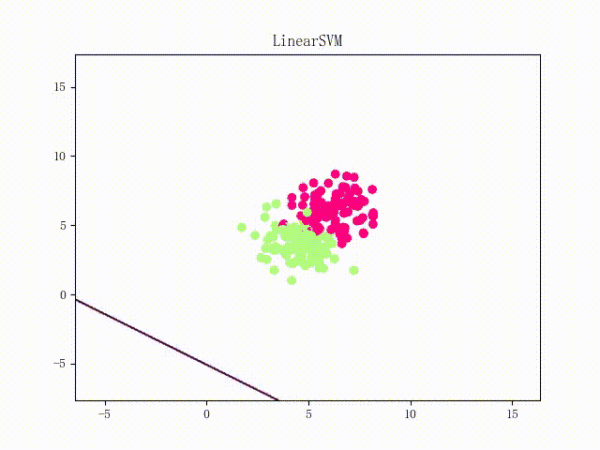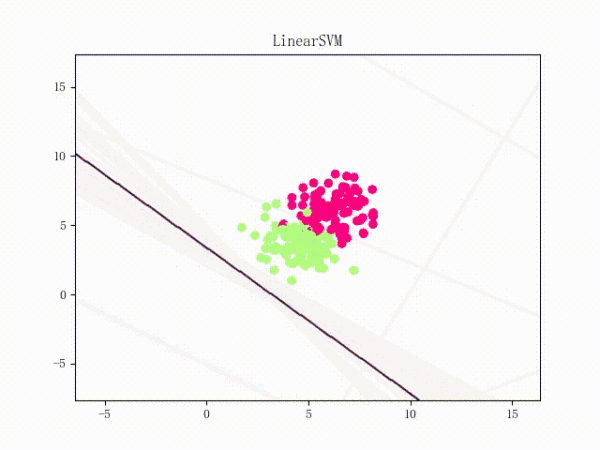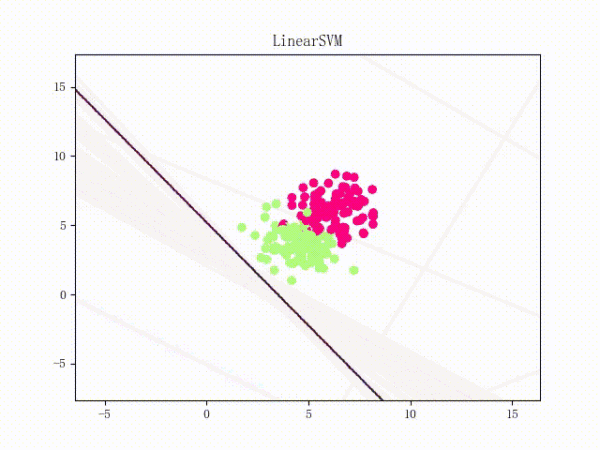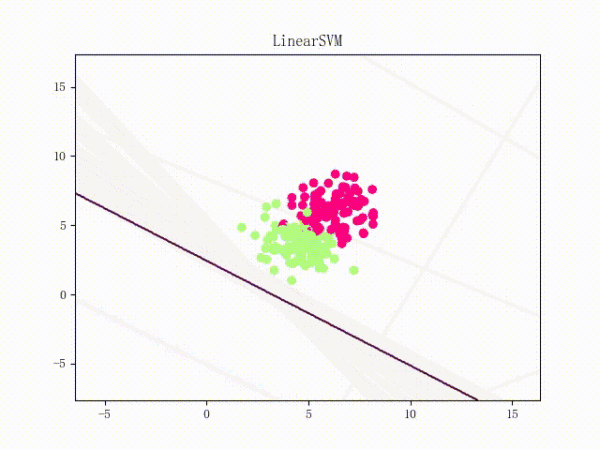
II.V.II. Mini-Batch 梯度下降法（MBGD）

解决方案的话，主要还是从改进随机梯度下降（SGD）的思路入手（因为极大梯度下降法其实就是 SGD 的特殊形式）。我们知道 SGD 的“升级版”是 MBGD、亦即拿随机 Mini-Batch 代替随机抽样。这样的话，通常而言会比 SGD 要好。

self._w *= 1 - lr
# 随机选取 batch_size 个样本
batch = np.random.choice(len(x), batch_size)
x_batch, y_batch = x[batch], y[batch]
err = 1 - y_batch * self.predict(x_batch, True)
if np.max(err) <= 0:
    continue
# 注意这里我们只能利用误分类的样本做梯度下降
# 因为被正确分类的样本处、这一部分的梯度为 0
mask = err > 0
delta = lr * c * y_batch[mask]
# 取各梯度平均并做一步梯度下降
self._w += np.mean(delta[..., None] * x_batch[mask], axis=0)
self._b += np.mean(delta)

但是问题仍然是存在的：那就是它们所运用的梯度下降法都只是朴素的 Vanilla Update，这会导致当数据的 scale 很大时模型对参数极为敏感、从而导致持续的震荡（所谓的 scale 比较大，可以理解为“规模很大”，或者直白一点——以二维数据为例的话——就是横纵坐标的数值很大）。

II.VI. Kernel Trick

注意，核函数技巧实际上并不是 SVM 的一部分。它可以与其他线性分类器共同使用，如逻辑回归等。支持向量机只负责找到决策边界。

以上我们求解的支持向量机都是在线性情况下的，那么非线性情况下如何处理？这里就引入：核方法²。

核方法是将一个低维的线性不可分的数据映射到一个高维的特征空间、并期望映射后的数据在高维特征空间里是线性可分的。

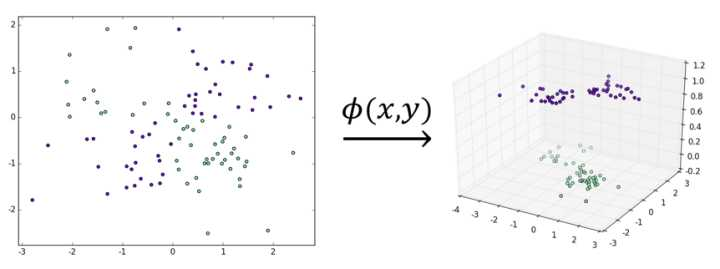
至此，似乎问题就转化为了如何寻找合适的映射\(\phi\)、使得数据集在被它映射到高维空间后变得线性可分。不过可以想象的是，现实任务中的数据集要比上文我们拿来举例的异或数据集要复杂得多、直接构造一个恰当的\(\phi\)的难度甚至可能高于解决问题本身。另外一个方面，这也会带来维度的急剧上升和很大的计算成本，使得模型求解效率大大下降。

而核方法的巧妙之处就在于，它能将构造映射这个过程再次进行转化、从而使得问题变得简易：它通过核函数来避免显式定义映射\(\phi\)。往简单里说，核方法会通过用能够表示成\(K(x_i,x_j)=\phi(x_i)\cdot\phi(x_j)\)的核函数\(K(x_i,x_j)\)替换各算式中出现的内积\(x_i\cdot x_j\)来完成将数据从低维映射到高维的过程。

假设\(x, z\in \mathbb{R}^n\), \(K(x,z)=(x^Tz)^2.\), 展开\(K(x,z)\):

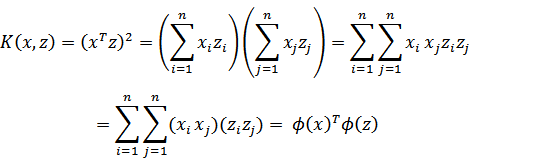
其中:

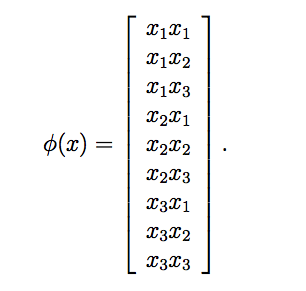
在这个例子中，映射后特征的内积和原始特征的内积的平方是等价的。也就是说，我们只需要计算原始特征的内积再进行平方就可以了，并不需要先得到映射后的特征再计算映射后特征的内积。计算原始特征内积的时间复杂度为\(\mathcal{O}(n)\), 而计算映射特征\(\phi(x)\)的时间复杂度为\(\mathcal{O}(x^2)\)。

\[ x^{(i)}\cdot x^{(j)}\longrightarrow \phi(x^{(i)})\cdot \phi(x^{(j)}) =K(x^{(i)},x^{(j)}) \]

映射函数 \(\phi\) 的作用是将低维空间的数据映射到高维空间中，核函数 \(K\) 表示的是映射之后高维空间中两个矢量的点积。

看一下这个列子：

\[ x=[x_1, x_2, x_3]^T,y=[y_1, y_2, y_3]^T \]

\[ \phi(x)=[x_1x_1,x_1x_2,x_1x_3,x_2x_1,x_2x_2,x_2x_3,x_3x_1,x_3x_2,x_3x_3] \]

\[ \begin{split} \phi(1,2,3)&=[1,2,3,2,4,6,3,6,9]^T\\ \phi(4,5,6)&=[16,20,24,20,25,30,24,30,36]^T\\ \phi(1,2,3) \cdot \phi(4,5,6) &=1\times16+2\times 20 + 3\times 24 + 2\times 20 + 4 \times 25 + 6 \times 30 + 3 \times 24 + 6 \times 30 + 9\times 36=1024 \end{split} \]

\[ \begin{split} \phi(x)\cdot \phi(y)&=[x_1x_1,x_1x_2,x_1x_3,x_2x_1,x_2x_2,x_2x_3,x_3x_1,x_3x_2,x_3x_3]^T\cdot [y_1y_1,y_1y_2,y_1y_3,y_2y_1,y_2y_2,y_2y_3,y_3y_1,y_3y_2,y_3y_3] \\ &= x_1y_1x_1y_1+x_1y_1x_2y_2+x_1y_1x_3y_3+x_2y_2x_1y_1+x_2y_2x_2y_2+x_2y_2x_3y_3\\&+x_3y_3x_1y_1+x_3y_3x_2y_2+x_3y_3x_3y_3\\ &=(x_1y_1+x_2y_2+x_3y_3)^2\\ &=(x^Ty)^2\\ &=K(x,y) \end{split} \]

\[ \begin{split} K(x,y)=K((1,2,3),(4,5,6))=(1\times 4 + 2\times 5 + 3\times 6)^2=(32)^2=1024 \end{split} \]

相比于从低维映射到高维空间再进行矢量积运算，核函数大大简化了计算的过程，使得向更高维转化变为了可能，我们不需要知道低维空间的数据是怎样映射到高维空间的，我们只需要知道结果是怎么计算出来的。

我们再来看另一个kernels:

\[ \begin{align} K(x,z) & =(x^Tz+c)^2 \\ & = \sum_{i,j=1}^n(x_ix_j)(z_iz_j) + \sum_{i=1}^n(\sqrt{2c}x_i)(\sqrt{2c}x_j)+c^2. \end{align} \]

更广泛的来说，我们有：\(K(x,z)=(x^Tz+c)^d\)，这个kernel将n维的特征映射为\({ {n+d} \choose d }\)维。

核方法的思想如下：

将算法表述成样本点内积的组合（这经常能通过算法的对偶形式实现）
设法找到核函数\(K(x_i,x_j)\)，它能返回样本点\(x_i、x_j\)被\(\phi\)作用后的内积
用\(K(x_i,x_j)\)替换\(x_i\cdot x_j\)、完成低维到高维的映射（同时也完成了从线性算法到非线性算法的转换）

如果我们有一个新的问题我们该如何构造一个kernel？假设我们有映射后的特征向量\(\phi(x)\)和\(\phi(z)\), kernel就是用来计算它们两之间的内积。如果\(\phi(x)\)和\(\phi(z)\)相似的话，即这两个向量的夹角很小，那么这个内积就会很大；相反地，如果它们差别很大，那么这个内积就会很小。所以，我们可以这样想kernels，当\(x\)和\(z\)相似时，\(K(x,z)\)很大。反之，当\(x\)和\(z\)不同时， \(K(x,z)\)很小。

我们再来看一个kernel:

\[ K(x,z)=exp\left(-\frac{||x-z||^2}{2\sigma^2}\right). \]

这个kernel应该挺符合上面的想法吧。这个kernel长得像高斯分布，我们一般叫他高斯kernel，也可以叫Radial basis funtction kernel，简称RBF核。

下面有张图说明在低维线性不可分时，映射到高维后就可分了，使用高斯核函数。

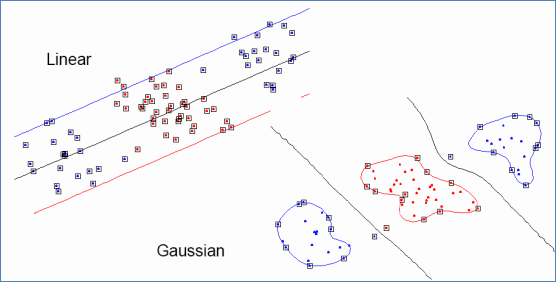
II.VI.I. 核函数有效性判定

并不是所有的函数\(K\)都能够对应一个映射（亦即不是所有的\(K(x_i,x_j)\)都能拆成\(\phi(x_i)\cdot\phi(x_j)\)；比如说，显然\(K(x_i,x_j)\)至少需要是一个对称函数）。

幸运的是，1909 年提出的 Mercer 定理解决了这个问题。Mercer 定理为寻找核函数带来了极大的便利。如果\(K\)是一个有效的kernel，那么对于在训练集上的核矩阵\(K\)一定是半正定的。事实上，这不仅仅是个必要条件，它也是充分条件。有效核也叫作Mercer Kernel。

Mercer 定理: 函数\(K\)是\(\mathbb{R}^n\times\mathbb{R}^n\to\mathbb{R}\)上的映射. 如果\(K\)是一个有效的(Mercer)Kernel, 那么当且仅当对于任意\(\lbrace x^{(1)},…,x^{(m)}\rbrace, (m\lt\infty)\), 相应的kernel matrix是半正定的。

\[K_{ij}=K(x^{(i)}, x^{(j)})=\phi(x^{(i)})^T\phi(x^{(j)})=\phi(x^{(j)})^T\phi(x^{(i)})=K(x^{(j)}, x^{(i)})=K_{ji}\]

那么核方法的应用场景有哪些呢？在 2002 年由 Scholkopf 和 Smola 证明的表示定理告诉我们它的应用场景非常广泛。

II.VII. Kernel SVM

因此，SVM 其实并不需要真正的向量，它可以用它们的数量积（点积）来进行分类。核函数可以减少大量的计算资源需求。通常，内核是线性的，所以我们得到了一个线性分类器。但如果使用非线性内核，我们可以在完全不改变数据的情况下得到一个非线性分类器：我们只需改变点积为我们想要的空间，SVM 就会对它忠实地进行分类。这意味着我们可以避免耗费计算资源的境地了。（直观可视化解释）。

为了完成这个目的，令 \(\phi(\mathbf x)\) 表示将 \(\mathbf x\) 映射后的特征向量，于是，在特征空间划分超平面所对应的模型可表示为：

\[ \sum_{k=1}^m\alpha_iy^{(i)}=0, w =\sum_{k=1}^m\alpha_iy^{(i)}x^{(i)} \\ y=w^Tx+b \]

\[ \begin{split} y&=\sum_{k=1}^m\alpha _ iy^{(i)}x^{(i)}x+b\\ &=\sum_{k=1}^m\alpha _ iy^{(i)}< x^{(i)},x >+b\\ \end{split} \]

\[ y=\sum_{k=1}^m\alpha_iy^{(i)} < \phi(x^{(i)}),\phi(x) > +b \]

\[ f(\mathbf x) = \mathbf w^T \phi(\mathbf x) + b \]

\[ y=\sum_{k=1}^m\alpha _ iy^{(i)}K(x^{(i)},x)+b\\ \]

在SVM的等价对偶问题中的目标函数中有样本点的内积\((x_i \cdot x_j)\)，，在空间变换后则是\((\phi(x_i) \cdot \phi(x_j))\) 。由于维数增加导致内积计算成本增加，这时核函数（kernel function）便派上用场了，将映射后的高维空间内积转换成低维空间的函数：\(K(x,z)=\phi(x) \cdot \phi(z)\)。

同理上文中引入拉格朗日乘子，求解整个方程后可得：

\[ \begin{align} f(\mathbf x) &= \mathbf w^T \phi(\mathbf x) + b \\ &= \sum_{i=1}^m \lambda_i y_i \phi(\mathbf x_i)^T \phi(\mathbf x) + b \\ &= \sum_{i=1}^m \lambda_i y_i k(\mathbf x,\mathbf x_i)+ b \end{align} \]

注意，使用核函数后，怎么分类新来的样本呢？是否先要找到\(\phi(\mathbf x)\)，然后再预测？答案肯定不是了。只需要根据上式的值判断即可，如果值大于等于1，那么是正类，小于等于是负类。在两者之间，认为无法确定。

这里的函数 \(k(\cdot,\cdot)\) 就是核函数（kernel function） ，常见的核函数见下表：

名称	表达式	参数
线性核	\(\boldsymbol x_i^T \boldsymbol x_j\)	无
多项式核	\((\boldsymbol x_i^T \boldsymbol x_j)^d\)	\(d \geqslant 1\) 多项式次数
高斯核	\(exp(-\frac{\lVert\boldsymbol x_i - \boldsymbol x_j \lVert^2}{2\sigma^2})\)	\(\sigma>0\) 高斯核带宽
拉普拉斯核	\(exp(-\frac{\lVert\boldsymbol x_i - \boldsymbol x_j \lVert^2}{\sigma})\)	\(\sigma>0\)
Sigmoid核	\(tanh(\beta \boldsymbol x_i^T\boldsymbol x_j + \theta)\)	\(\beta>0\) \(\theta>0\)

II.VII.I. 感知器核方法

怎么应用核方法？简单来说，就是把算法中涉及到样本（\(x_i\)）的地方都通过某种变换、弄成样本的内积形式（\(x_i\cdot x_j\)）。

感知机的原始损失函数为

\[ L(D) = \sum_{i=1}^N\left[ -y_i(w\cdot x_i+b)\right]_ + \]

为了让损失函数中的样本都变成内积形式，考虑令\(w = \sum_{i=1}^N\alpha_ix_i\)（也有令\(w = \sum_{i=1}^N\alpha_iy_ix_i\)的），则

\[ \begin{align} L(D) &= \sum_{i=1}^N\left[ -y_i\left[\left(\sum_{j=1}^N\alpha_jx_j\right)\cdot x_i+b\right]\right]_ + \\ &= \sum_{i=1}^N\left[ -y_i\left(\sum_{j=1}^N\alpha_j(x_i\cdot x_j)+b\right)\right]_ + \end{align} \]

在此之上应用核方法是平凡的：设核函数为\(K\)，只需把所有的\(x_i\cdot x_j\)换成\(K(x_i,x_j)\)即可：

\[ L(D) = \sum_{i=1}^N\left[ -y_i\left(\sum_{j=1}^N\alpha_jK(x_i,x_j)+b\right)\right]_ + \]

于是优化问题变为

\[ \min_{\alpha}\sum_{i=1}^N\left[ -y_i\left(\sum_{j=1}^N\alpha_jK(x_i,x_j)+b\right)\right]_ + \]

预测步骤则变为

\[ y_{\text{pred}}=w\cdot x+b=\sum_{i=1}^N\alpha_iK(x_i, x)+b \]

当我们对感知机应用核方法后，它就能对非线性数据集（比如螺旋线数据集）进行分类了。

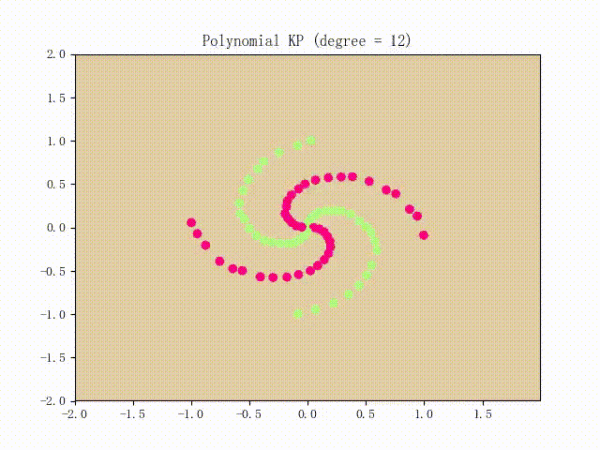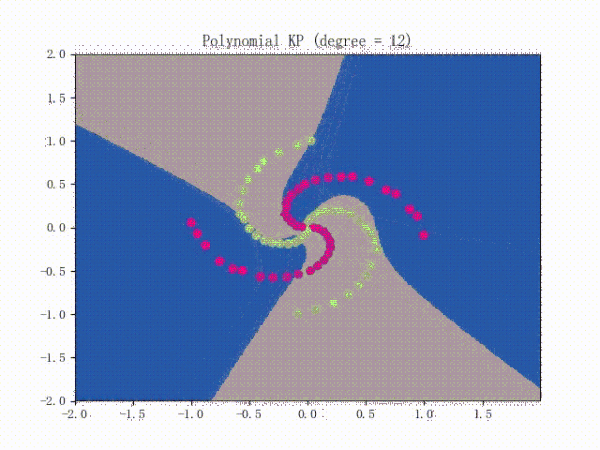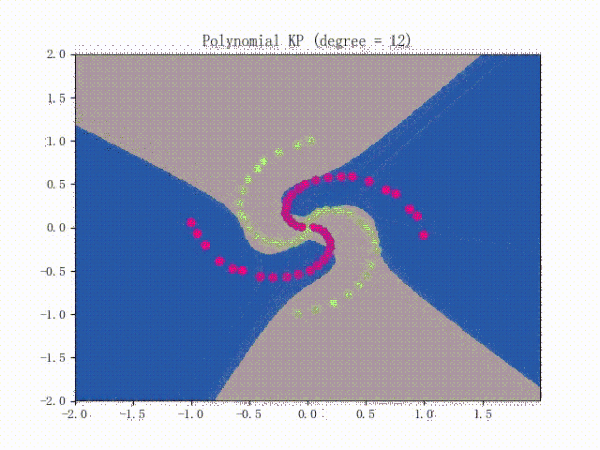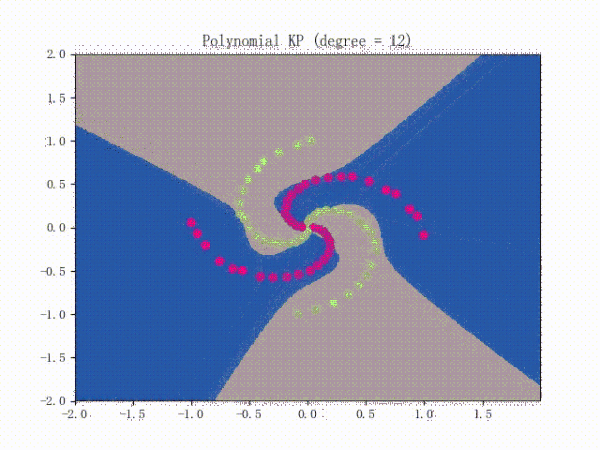
II.VII.II. Soft Kernel SVM

将其代入一般化的SVM学习算法的目标函数中，可得非线性SVM的最优化问题：

\[ L(D)=\frac12\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jK(x_i,x_j)+C\sum_{i=1}^N\left[ 1-y_i\left(\sum_{j=1}^N\alpha_jK(x_i,x_j)+b\right)\right]_ + \]

\[ \begin{align} \min_{\alpha} \quad \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j K(x_i,x_j) - \sum_{i=1}^{N}\alpha_i \\ s.t. \quad \sum_{i=1}^{N}\alpha_i y_i = 0 ; \quad 0 \le \alpha_i \le C, \quad i=1,2,\cdots,N \end{align} \]

预测步骤则仍然是：

\[ y_{\text{pred}}=w\cdot x+b=\sum_{i=1}^N\alpha_iK(x_i, x)+b \]

II.VIII. 核方法的训练

核感知机的梯度下降法

SMO算法的效果

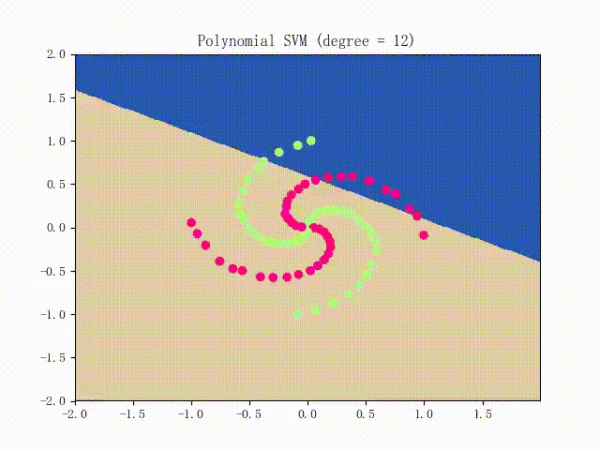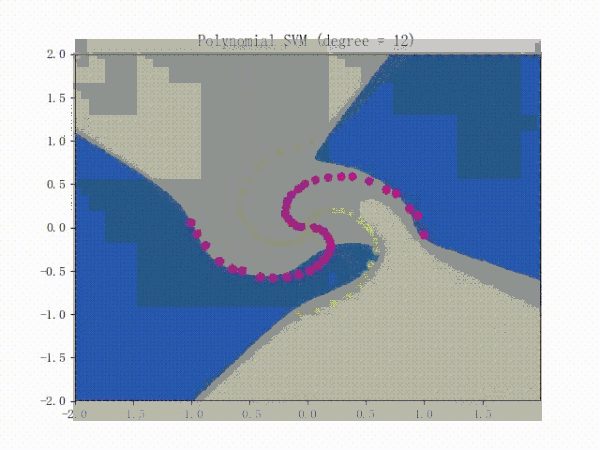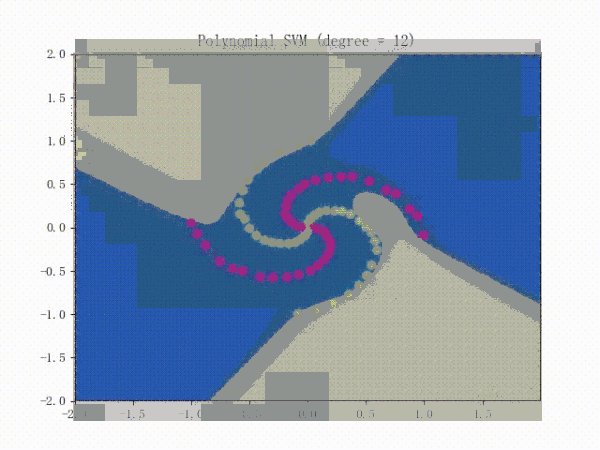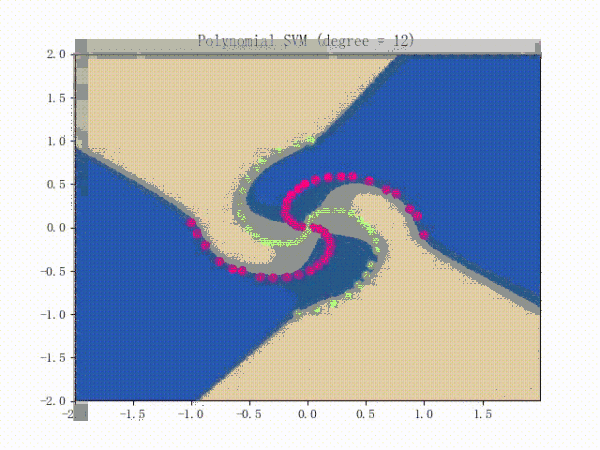
III. SVR

对SVM解回归问题，进行分析。

【机器学习详解】SVM解回归问题

IV. 扩展应用

当数据未被标记时，不能进行监督式学习，需要用非监督式学习，它会尝试找出数据到簇的自然聚类，并将新数据映射到这些已形成的簇。将支持向量机改进的聚类算法被称为支持向量聚类，当数据未被标记或者仅一些数据被标记时，支持向量聚类经常在工业应用中用作分类步骤的预处理。

V. MATLAB实现

得到数值temp1：

1 2	cmd = ['-v ',num2str(v),' -c ',num2str(ga_bestc),' -g ',num2str(ga_bestg),' -s 3 -p 0.01']; temp1 = svmtrain(train_label,train_data,cmd);

得到训练的模型temp2：

1 2	cmd = ['-t 2',' -c ',num2str(ga_bestc),' -g ',num2str(ga_bestg),' -s 3 -p 0.01']; temp2 = svmtrain(train_label,train_data,cmd);

livsvm的svr验证：

% 训练集输入
[pn_train,inputps] = mapminmax(p_train');
pn_train = pn_train';
% 测试集输入
pn_test = mapminmax('apply',p_test',inputps);
pn_test = pn_test';
% 训练集预测验证
t_svr_train = zeros(len_train,1);
for i = 1:len_train
    x = pn_train(i,:);
    t_svr_train (i,1) = SVRDecisionFunction(x,gs_model);
end
% 反归一化
t_svr_train_1 = mapminmax('reverse',t_svr_train,outputps);
% 测试集预测验证
t_svr_test = zeros(len_test,1);
for i = 1:len_test
    x = pn_test(i,:);
    t_svr_test (i,1) = SVRDecisionFunction(x,gs_model);
end
% 反归一化
t_svr_test_1 = mapminmax('reverse',t_svr_test,outputps);

figure
hold on
h200=plot(1:length(set_num),[t_train;t_test]','r-o');
h202=plot(1:length(set_num),[gs_predict_1;gs_predict_2]','b-+');
h203=plot(1:length(set_num),[t_svr_train_1;t_svr_test_1]','g-+');

VI. SVM 参数优化

In support vector machines (SVM) how can we adjust the parameter C?

C is a trade-off between training error and the flatness of the solution. The larger C is the less the final training error will be. But if you increase C too much you risk losing the generalization properties of the classifier, because it will try to fit as best as possible all the training points (including the possible errors of your dataset). In addition a large C, usually increases the time needed for training.

If C is small, then the classifier is flat (meaning that its derivatives are small - close to zero, at least for the gaussian rbf kernel this is substantiated theoretically). You have to find a C that keeps the training erro small, but also generalizes well (i.e., it doesn't have large fluctuations). There are several methods to find the best possible C automatically, but you must keep in mind that this depends on the application you are interested in.