协方差矩阵

更新于 分类： 阅读次数： 本文字数： 826 阅读时长 ≈ 3 分钟

在统计学与概率论中，协方差矩阵（也称离差矩阵、方差-协方差矩阵）是一个矩阵，其 i, j 位置的元素是第 i 个与第 j 个随机向量（即随机变量构成的向量）之间的协方差。这是从标量随机变量到高维度随机向量的自然推广。

首先定义一个含有n个样本的集合\(X=\{X_1,\ldots,X_n\}\)，

  • 均值：\(\bar{X}=\frac{\sum_{i=1}^n X_{i}}{n}\)
  • 标准差：\(s=\sqrt{\frac{\sum_{i=1}^n (X_{i}-\bar{X})^2}{n-1}}\)
  • 方差：\(s^2=\frac{\sum_{i=1}^n (X_{i}-\bar{X})^2}{n-1}\)

均值描述的是样本集合的中间点，它告诉我们的信息是很有限的，而标准差给我们描述的则是样本集合的各个样本点到均值的距离之平均。标准差描述的就是这种“散布度”。之所以除以\(n-1\)而不是除以\(n\)，是因为这样能使我们以较小的样本集更好的逼近总体的标准差，即统计上所谓的“无偏估计”。

但我们应该注意到，标准差和方差一般是用来描述一维数据的，但现实生活我们常常遇到含有多维数据的数据集。协方差就是这样一种用来度量两个随机变量关系的统计量，我们可以仿照方差的定义：

\[var(X)=\frac{\sum_{i=1}^n (X_{i}-\bar{X})(X_{i}-\bar{X})}{n-1}\]

来度量各个维度偏离其均值的程度，标准差可以这么来定义：

\[cov(X,Y)=cov(Y,X)=var(X)=\frac{\sum_{i=1}^n (X_{i}-\bar{X})(Y_{i}-\bar{Y})}{n-1}\]

如果结果为正值，则说明两者是正相关的(从协方差可以引出“相关系数”的定义)。如果为0，也是就是统计上说的“相互独立”。

协方差也只能处理二维问题，那维数多了自然就需要计算多个协方差，比如\(n\)维的数据集就需要计算\(\frac{n!}{(n-2)!* 2}\)个协方差，那自然而然的我们会想到使用矩阵来组织这些数据。给出协方差矩阵的定义：

\[C_{n\times n}=(c_{i,j},c_{i,j}=cov(Dim_{i},Dim_{j}))\]

假设数据集有\(\{x,y,z\}\)三个维度，则协方差矩阵为

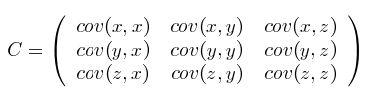
可见，协方差矩阵是一个对称的矩阵，而且对角线是各个维度上的方差。协方差矩阵计算的是不同维度之间的协方差，而不是不同样本之间的。

I. MATLAB 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
% 方法一
MySample = fix(rand(10,3)*50)
dim1 = MySample(:,1);
dim2 = MySample(:,2);
dim3 = MySample(:,3);
sum( (dim1-mean(dim1)) .* (dim2-mean(dim2)) ) / ( size(MySample,1)-1 )
% 得到  74.5333
sum( (dim1-mean(dim1)) .* (dim3-mean(dim3)) ) / ( size(MySample,1)-1 )
% 得到  -10.0889
sum( (dim2-mean(dim2)) .* (dim3-mean(dim3)) ) / ( size(MySample,1)-1 )
% 得到  -106.4000
std(dim1)^2 % 得到   108.3222
std(dim2)^2 % 得到   260.6222
std(dim3)^2 % 得到   94.1778

% 方法二
% 先让样本矩阵中心化，即每一维度减去该维度的均值，使每一维度上的均值为0
% 然后直接用新的到的样本矩阵乘上它的转置，然后除以(N-1)即可。
X = MySample - repmat(mean(MySample),10,1);
% 中心化样本矩阵，使各维度均值为0
C = (X'*X)./(size(X,1)-1);

% 方法三
cov(MySample)