机器学习中的信息论

更新于 分类： 阅读次数： 本文字数： 4.4k 阅读时长 ≈ 16 分钟

信息论是应用数学的一个分支，主要研究的是对一个信号包含信息的多少进行量化。它最初被发明是用来研究在一个含有噪声的信道上用离散的字母表来发送消息，例如通过无线电传输来通信。，一般在机器学习中，我们可以将信息论应用在连续型变量上，并使用信息论的一些关键思想来描述概率分布或者量化概率分布之间的相似性。

在信息论中，熵是对不确定性的一种度量。信息量越大，不确定性就越小，熵也就越小；信息量越小，不确定性越大，熵也越大。根据熵的特性，可以通过计算熵值来判断一个事件的随机性及无序程度，也可以用熵值来判断某个指标的离散程度，指标的离散程度越大，该指标对综合评价的影响（权重）越大。比如样本数据在某指标下取值都相等，则该指标对总体评价的影响为0，权值为0.

从香农熵到手推KL散度：一文带你纵览机器学习中的信息论

I. 熵

Entropy来源于希腊语，原意：内向，即：一个系统不受外部干扰时往内部稳定状态发展的特性。熵是热力学的一个物理概念，定义的其实是一个热力学的系统变化的趋势

\[\Delta S = \frac{Q}{T} = \frac{热量}{温度} \tag{1-1}\]

  • 广义的定义：熵是描述一个系统的无序程度的变量；同样的表述还有，熵是系统混乱度的度量，一切自发的不可逆过程都是从有序到无序的变化过程，向熵增的方向进行。熵越大说明系统越混乱，携带的信息越少，熵越小说明系统越有序，携带的信息越多。

  • 信息论中，熵是接受的每条消息中包含的信息的平均值。又被称为信息熵、信源熵、平均自信息量。

1923年，德国科学家普朗克来中国讲学用到entropy这个词，胡刚复教授看到这个公式，创造了“熵”字，因为“火”和热量有关，定义式又是热量比温度，相当自洽。

II. 自信息

香农熵的基本概念就是所谓的一个事件背后的自信息（self-information），有时候也叫做不确定性。自信息的直觉解释如下，当某个事件（随机变量）的一个不可能的结果出现时，我们就认为它提供了大量的信息。相反地，当观察到一个经常出现的结果时，我们就认为它具有或提供少量的信息。将自信息与一个事件的意外性联系起来是很有帮助的。

III. 信息熵

在机器学习中，通常要把与随机事件相关信息的期望值进行量化，此外还要量化不同概率分布之间的相似性。在这两种情况下，香农熵都被用来衡量概率分布中的信息内容。

香农熵是以信息论之父 Claude Shannon 的名字命名的，也称为信息熵或微分熵（连续）。信息熵则借鉴了热力学中熵的概念 (注意：信息熵的符号与热力学熵应该是相反的)，用于描述平均而言事件信息量大小。1948年，由克劳德·爱尔伍德·香农将热力学中的熵引入信息论，所以也叫做：香农熵。

比如天气情况，假设可能有【阴、晴、雨、雪】四种情况，使用概率符号表示 \(\mathbf P = [p_1,p_2,p_3,p_4]\)，接下来自然而然的思考：那么，什么条件（情况）会影响这些值呢？假设有以下三种描述，或者说条件

  • 今天是晴天，所以明天可能也是晴天
  • 天气预报说明天下雨
  • 9月12日苹果公司举行发布会

那么这三个描述中，很明显，第二条的信息量更大，因为它可以使得不确定事件发生在\(p_3\)的概率更大。类似的，第三条对判断毫无帮助，信息量为0。注意，信息量不等于信息熵，如果是这样，那么直接用概率来衡量就可以了，不需要在重新定义一个概念。

所以数学上，信息熵是事件所包含的信息量的期望（均值）1。它不是针对每条信息，而是针对整个不确定性结果集而言，信息熵越大，信源的分布越随机，事件不确定性就越大。单条信息只能从某种程度上影响结果集概率的分布.

在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和。根据上面期望的定义，我们可以设想信息熵的公式大概是这样的一个格式：

\[信息熵=\sum 每种可能事件的概率 * 每种可能事件包含的信息量\]

那么每种可能事件包含的信息量跟什么有关呢？答案是跟这一事件的不确定性有关，即与事件发生的概率有关，概率越大，信息量越小。试想，如果上面的概率修改一下，令小明得100分的概率是1，那么你预测小明会考100分这句话就没有信息量了，因为不管怎么样他肯定都会是100分。

我们已经有了 \(\mathbf P = [p_1,p_2,p_3,p_4]\) 来表示天气情况，那么用计算机来存储每天的天气，那该如何编码呢？常见的做法是，4个不同的信息，只需要2bit就能做到，00 01 11 10 。

使用一个公式来计算记录n天数据需要的存储空间：

\[ S_n = n \times \sum_{i = 1}^4{\left(P_i \times F(P_i) \right) } \tag{2-1} \]

\(P_i\) 表示第i个事件发生的概率；\(F(P_i)\) 表示存储空间的存储因子（每种可能事件包含的信息量的计算采用不确定性函数）.

如何确定这个函数 \(F(P_i)\) 的形式？考虑这个函数需要满足条件：概率大的事件对应小的存储空间，说人话，就是成反比，你的数学功底不错的话，脑海中第一反应出来满足这个条件最直观是反比例函数，说人话， \(\frac{1}{P_i}\) 。之后我们发现这个公式中有个除法非常讨厌，我们想着去掉它，脑海中第一反应出来的满足这个条件的一定是取对数，至于为什么取对数，那说道就很多，取对数是指数的逆操作，

  • 对数操作可以让原本不符合正态分布的模型符合正态分布，比如随着模型自变量的增加，因变量的方差也增大的模型取对数后会更加稳定
  • 取对数操作可以rescale（原谅我，这里思前想后还是感觉一个英文单词更加生动）其实本质来说都是因为第一点。说人话版本，人不喜欢乘法，对数可以把乘法变加法

那么我们结束清楚之后，就很容易就可以定义出（ 采用这个函数，一方面保证了信息量是概率P的单调递降函数；另一方面保证了两个独立事件所产生的不确定性应等于各自不确定性之和，即可加性。）

\[F(P_i) = \log_a ({\frac{1}{P_i}}) \tag{2-2}\]

a作为底数，可以取2（处理2bit数据），10（万金油），e（处理正态分布相关的数据）

结合对信息熵的定义（第一节最后的粗体字）然后把（2-2）带入（2-1），就会发现，哦！看着有点眼熟啊

\[H(P) = \sum_i {P(i)log_a {\frac{1}{P(i)}}} = - \sum_i {P(i)log_a {P(i)}} \tag{2-3}\]

\[H(U) = -\sum_{i=1}^{n} P_i logP_i\]

总结就发现，信息熵其实从某种意义上反映了信息量存储下来需要多少存储空间。总结为：根据真实分布，我们能够找到一个最优策略，以最小的代价消除系统的不确定性（比如编码），而这个代价的大小就是信息熵。

IV. 熵值法

熵值法确定权重的步骤及适用范围
【评价算法】01. 熵权法确定权重

日常工作中经常需要确定各个指标的权重，利用熵值法确定权重属于客观赋权法，从数据出发，仅依赖于数据本身的离散性，避免过强的主观性。

根据信息熵的定义，对于某项指标，我们可以用熵值来判断某个指标的离散程度，其熵值越小，指标的离散程度越大，该指标对综合评价的影响(即权重)越大。如果某项指标的值全部相等，那么该指标在综合评价中不起作用。

熵值法的计算步骤:

  1. 确定指标体系：首先需要确定评价的指标体系，例如下图是网站经营评价的两级指标体系。

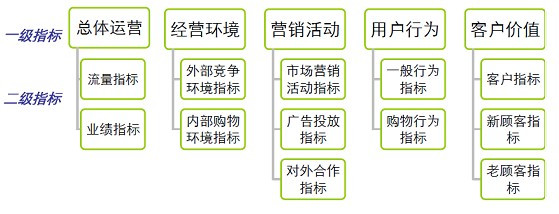
  2. 清洗指标极值：即剔除各指标中极大或者极小的值，一般用比较合理的上下线替换这些极值，目的是减少极值数据对该指标的熵的影响。 原则：剔除占样本总数不到1-2%但指标值贡献率超过20-30%以上的极值样本。 我们这里样本本来也不多，也没有贡献率特别大的，所以没有做处理。

  3. 归一化指标处理：由于各项指标的计量单位并不统一，因此在用它们计算综合指标前，先要进行标准化处理，即把指标的绝对值转化为相对值，从而解决各项不同质指标值的同质化问题。另外，正向指标和负向指标数值代表的含义不同（正向指标数值越高越好，负向指标数值越低越好），因此，对于正向负向指标需要采用不同的算法进行数据标准化处理：将各个指标同度量化，即将指标的实际值转化为不受量纲影响的指标评价值。常用的方法有：
    • 临界值法:如果原始的第\(i\)个人的第\(j\)个指标是\(x_{ij}\)，那么归一化后是\(x_{ij}’\)。若指标是正向的选第一个公式； 若指标是负向的选第二个公式。\(\min x_j\)是第\(j\)个指标的最小值，类似地，\(\max x_j\)是第\(j\)个指标的最大值。

    \[x_{ij}’ = \frac{x_{ij}-\min x_j}{\max x_j - \min x_j}\] \[x_{ij}’ = \frac{\max x_j-x_{ij}}{\max x_j - \min x_j}\]

    • Z-score法: \(x_{ij}’ = \frac{x_{ij}-\bar{x_j}}{S}\)

  4. 计算指标熵和权：

    • 计算指标熵要先计算第\(i\)个人的第\(j\)个指标值的比重 \(y_{ij} = \frac{x_{ij}’}{\sum_{i=1}^m {x_{ij}’}}\)
    • 计算第j项指标的信息熵的公式为 \(e_j = -K\sum_{i=1}^m y_{ij} \ln y_{ij}\) (式中\(K\)为常数，\(K=\frac{1}{\ln m}\)，我觉得乘以这个主要是为了使得\(e_j\)小于等于1，这样后面求得的权重才是正数)
    • 某项指标的信息效用价值取决于该指标的信息熵\(e_j\)与1之间的差值，它的值直接影响权重的大小，信息效用值越大，对评价的重要性就越大，权重也就越大。直接影响权重的大小，信息效用值越大，对评价的重要性就越大，权重也就越大。值直接影响权重的大小，信息效用值越大，对评价的重要性就越大，权重也就越大。直接影响权重的大小，信息效用值越大，对评价的重要性就越大，权重也就越大。\(d_j = 1 - e_j\)
    • 第\(j\)项指标的权重为\(w_j = \frac{d_j}{\sum_j d_j}\)

  5. 指标加权计算得分：最后一步就是利用加权求和公式计算样本的评价值了，\(U = \sum_j 100* y_{ij}w_j\)，\(U\)为综合评价值，\(w_j\)为第j个指标的权重。

IV.I. Matlab实现

1
2
3
4
5
load shang_datas

Ind=[1 1 1 1 2]; %指定各指标的正向or负向

[S,W]=shang(X,Ind)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
function [s,w]=shang(x,ind)
%实现用熵值法求各指标(列）的权重及各数据行的得分
%x为原始数据矩阵, 一行代表一个样本, 每列对应一个指标
%ind指示向量，指示各列正向指标还是负向指标，1表示正向指标，2表示负向指标
%s返回各行（样本）得分，w返回各列权重
[n,m]=size(x); % n个样本, m个指标
%%数据的归一化处理
for i=1:m
    if ind(i)==1 %正向指标归一化
        X(:,i)=guiyi(x(:,i),1,0.002,0.996);    %若归一化到[0,1], 0会出问题
    else %负向指标归一化
        X(:,i)=guiyi(x(:,i),2,0.002,0.996);
    end
end
%%计算第j个指标下，第i个样本占该指标的比重p(i,j)
for i=1:n
    for j=1:m
        p(i,j)=X(i,j)/sum(X(:,j));
    end
end
%%计算第j个指标的熵值e(j)
k=1/log(n);
for j=1:m
    e(j)=-k*sum(p(:,j).*log(p(:,j)));
end
d=ones(1,m)-e; %计算信息熵冗余度
w=d./sum(d); %求权值w
s=100*w*p'; %求综合得分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
function y=guiyi(x,type,ymin,ymax)
%实现正向或负向指标归一化，返回归一化后的数据矩阵
%x为原始数据矩阵, 一行代表一个样本, 每列对应一个指标
%type设定正向指标1,负向指标2
%ymin,ymax为归一化的区间端点
[n,m]=size(x);
y=zeros(n,m);
xmin=min(x);
xmax=max(x);
switch type
    case 1
        for j=1:m
            y(:,j)=(ymax-ymin)*(x(:,j)-xmin(j))/(xmax(j)-xmin(j))+ymin;
        end
    case 2
        for j=1:m
            y(:,j)=(ymax-ymin)*(xmax(j)-x(:,j))/(xmax(j)-xmin(j))+ymin;
        end
end

IV.II. 熵值法的优缺点及适用范围

优点

  • 熵值法能深刻反映出指标的区分能力，进而确定权重
  • 是一种客观赋权法，有理论依据，相对主观赋权具有较高的可信度和精确度
  • 算法简单，实践起来比较方便，不需要借助其他分析软件

缺点

  • 智能程度不够高。和多元回归和主成分等统计方法不同，它不能考虑指标与指标之间横向的影响（如：相关性）
  • 若无业务经验的指导，权重可能失真
  • 对样本的依赖性比较大，随着建模样本变化，权重会有一定的波动

适用范围

结合上面的实例，我们看到：体育成绩离散程度更大，导致其最后权重也更大，但是从通常评判的角度看，聪明程度往往与数学成绩关系更为密切。这就说明单单使用熵值法权重失真是经常发生的，要结合一定专家打分法才能发挥熵值法的优势，像确定指标体系中的示意图那样，构建两级评价体系，上层可能需要结合专家经验来构建，而底层的指标分的比较细，权重比较难确定，这种情况下采用熵值法比较合适。

另外，确定权重前需要确定指标对目标得分的影响方向，对非线性的指标要进行预处理或者剔除。还要注意处理好极值。

V. 交叉熵

【直观详解】信息熵、交叉熵和相对熵

交叉熵是一个用来比较两个概率分布 p 和 q 的数学工具。它和熵是类似的，我们计算 log(q) 在概率 p 下的期望，而不是反过来。

VI. 相对熵

浅谈KL散度
相对熵（互熵，交叉熵，鉴别信息，Kullback熵，Kullback-Leible散度即KL散度）的深入理解
如何理解K-L散度（相对熵）
关于相对熵（KL距离）的理解

与交叉熵紧密相关，KL 散度是另一个在机器学习中用来衡量相似度的量。相对熵又称互熵，交叉熵，鉴别信息，Kullback熵，Kullback-Leible散度（即KL散度）等。

交叉熵衡量的是用编码方案 q 对服从 p 的事件进行编码时所需 bit 数的平均值，而 KL 散度给出的是使用编码方案 q 而不是最优编码方案 p 时带来的额外 bit 数。从这里我们可以看到，在机器学习中，p 是固定的，交叉熵和 KL 散度之间只相差一个常数可加项，所以从优化的目标来考虑，二者是等价的。而从理论角度而言，考虑 KL 散度仍然是有意义的，KL 散度的一个属性就是，当 p 和 q 相等的时候，它的值为 0。

KL 散度有很多有用的性质，最重要的是它是非负的。在李弘毅的讲解中，KL 散度可以从极大似然估计中推导而出。

  1. 信息熵是什么？↩