Long short-term memory

更新于 分类： 阅读次数： 本文字数： 536 阅读时长 ≈ 2 分钟

LSTM算法全称为Long short-term memory，最早由 Sepp Hochreiter和Jürgen Schmidhuber于1997年提出，是一种特定形式的RNN（Recurrent neural network，循环神经网络），而RNN是一系列能够处理序列数据的神经网络的总称。

I. 推导

关于lstm，有个非常好的博客。

前向更新公式为：

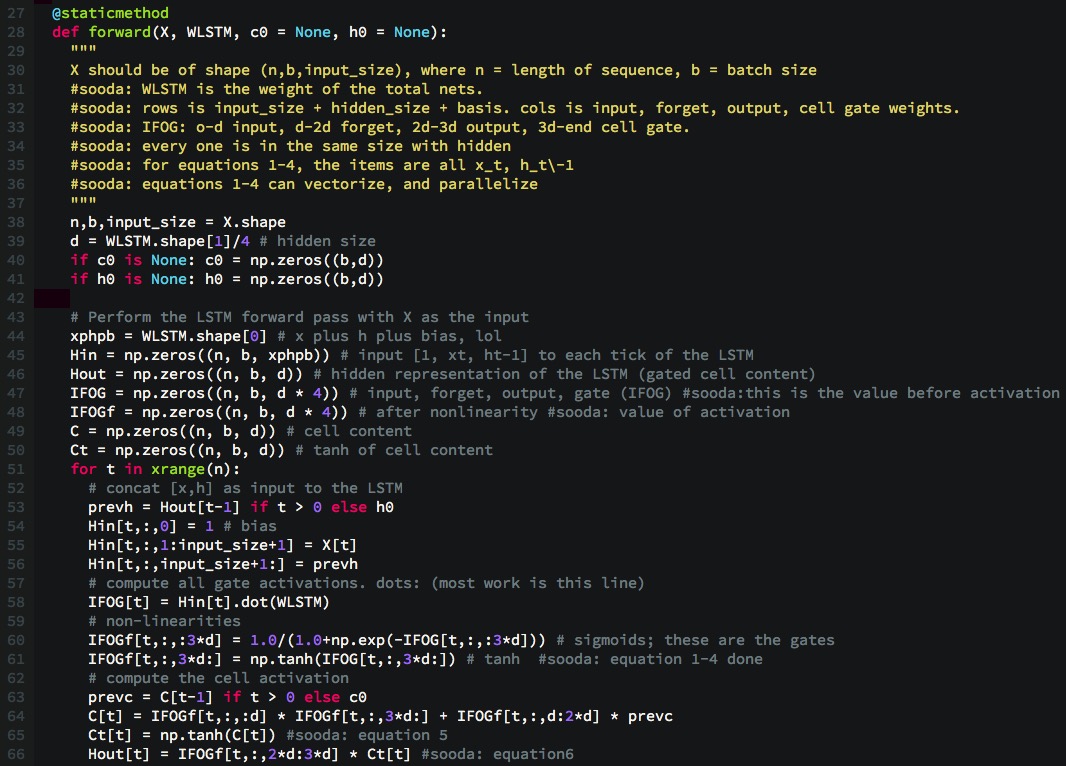
image

依照上文的后向传播的推导方式，可以得到， 前向更新，请见代码中#sooda注释部分：

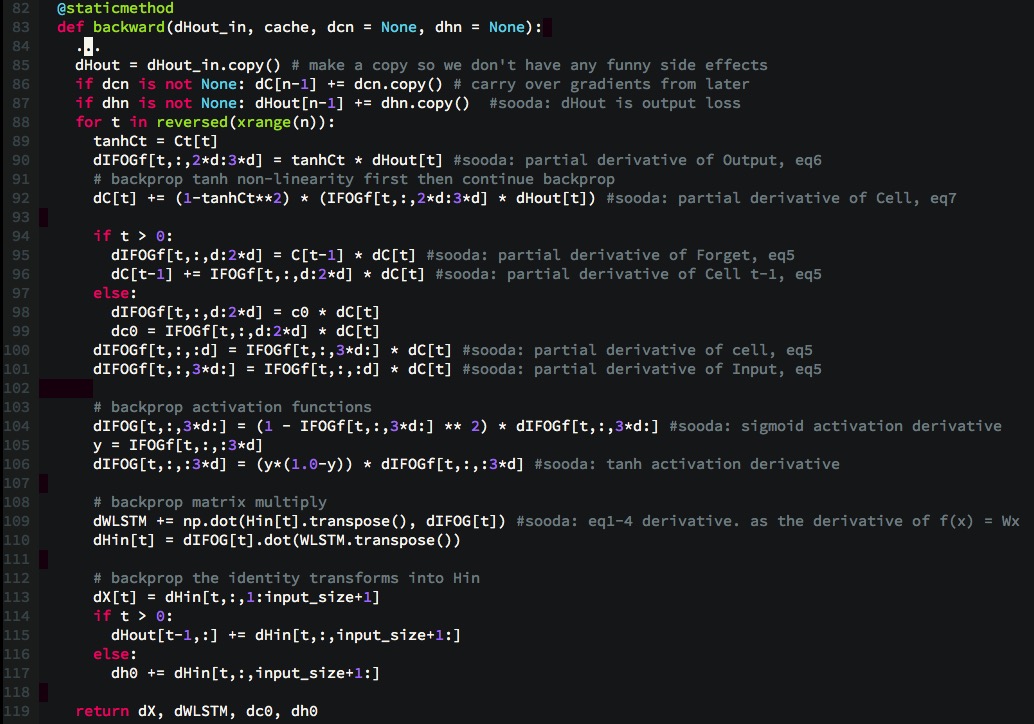
image

后向更新：

image

注意点:

  1. 通过观察公式1到4， 发现所有的乘机因子为x、h，互相没有依赖，可以并行化。利用向量化进行加速
  2. IFOG指的是Input，Forget， Output， Cell Gate的计算值。IFOGf是IFOG经过激活函数后的激活值. 并以此为顺序。o-d表示input gate， d-2d表示forget gate， 2d-3d表示output gate， 3d-end 表示cell gate
  3. WLSTM保存的实际上是所有这些门相对于输入+隐藏层+偏置的权值。
  4. 后向传播从最后一个进行求偏导， 即按照从后向前，按部就班即可，不需要跨步骤考虑
  5. cache是为了保存后向传播所需要的值

本文代码可以参考gist

I.I. 反向传播

LSTM的后向推导说是推导，基本上没有一个公式。注重理解。

cs231上有一篇关于非常好的文章, 讲得非常好。 一个例子： \[f(x,y) = \frac{x + \sigma(y)}{\sigma(x) + (x+y)^2}\]

1
2
3
4
5
6
7
8
9
10
11
x = 3 # example values
y = -4
# forward pass
sigy = 1.0 / (1 + math.exp(-y)) # sigmoid in numerator   #(1)
num = x + sigy # numerator                               #(2)
sigx = 1.0 / (1 + math.exp(-x)) # sigmoid in denominator #(3)
xpy = x + y                                              #(4)
xpysqr = xpy**2                                          #(5)
den = sigx + xpysqr # denominator                        #(6)
invden = 1.0 / den                                       #(7)
f = num * invden # done!                                 #(8)

对应的后向传播为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# backprop f = num * invden
dnum = invden # gradient on numerator                             #(8)
dinvden = num                                                     #(8)
# backprop invden = 1.0 / den
dden = (-1.0 / (den**2)) * dinvden                                #(7)
# backprop den = sigx + xpysqr
dsigx = (1) * dden                                                #(6)
dxpysqr = (1) * dden                                              #(6)
# backprop xpysqr = xpy**2
dxpy = (2 * xpy) * dxpysqr                                        #(5)
# backprop xpy = x + y
dx = (1) * dxpy                                                   #(4)
dy = (1) * dxpy                                                   #(4)
# backprop sigx = 1.0 / (1 + math.exp(-x))
dx += ((1 - sigx) * sigx) * dsigx # Notice += !! See notes below  #(3)
# backprop num = x + sigy
dx += (1) * dnum                                                  #(2)
dsigy = (1) * dnum                                                #(2)
# backprop sigy = 1.0 / (1 + math.exp(-y))
dy += ((1 - sigy) * sigy) * dsigy                                 #(1)
# done! phew