MATLAB使用指南
MATLAB(矩阵实验室)是MATrix LABoratory的缩写,是一款由美国The MathWorks公司出品的商业数学软件。MATLAB是一种用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境。除了矩阵运算、绘制函数/数据图像等常用功能外,MATLAB还可以用来创建用户界面及与调用其它语言(包括C,C++,Java,Python和FORTRAN)编写的程序。本文主要介绍MATLAB中常用命令,方便规范使用。
MATLAB 的替代品:
- Python是一门完全免费的通用编程语言,以开源的方式提供了大量各类用途的库与包,如 Numpy (数值计算)、 SciPy (数学、科学和工程计算)、 Matplotlib (类似MATLAB中plot的绘图工具)等等。
- Octave是GNU项目成员之一,提供了与MATLAB语法兼容的开放源代码科学计算及数值分析的工具。
- 对于航天器轨道计算、任务分析等,可以尝试General Mission Analysis Tool (GMAT)。GMAT提供了图像化界面或脚本两种接口,相比于STK,GMAT的深空探测相关功能更加强大,可配置的资源也更多。
- GNU Radio是一个对学习,构建和部署软件定义无线电系统的免费软件工具包,可通过Python或类似于Simulink/Labview的图形化界面调用。 紫丁香、龙江等卫星的业余无线电接收解调软件就是在GNU Radio基础上开发并开源发布的。
- Robot Operating System (ROS)是一种针对于满足不同机器人软件协同工作的灵活软件框架。目的在于提高软件模块化能力和复用能力,并实现不同任务间的数据/信号量的有效共享,方便多种机器人平台之间创建复杂和鲁棒的机器人行为,同时它也是一种工具库的约定与集合。
下载链接: https://www.iemblog.com/?s=matlab
I. 随机数
Matlab中的rand()函数产生的是伪随机数,但一般用来也可以接受。但是,如果我们知道伪随机数的初始状态,那么产生的伪随机数是唯一确定的。问题来了,Matlab每次启动会重置rand()和randn()的初始状态(重置为0),也就是说,你产生的随机数会出现两次随机数一模一样的情况。
1 | >> rand('state',0) |
设定初始状态的好处是,只需要保存那时的初始状态再运行一遍程序你就可以重现之前的计算过程和结果。缺点是虽然程序使用了随机数,但由于(每次启动后)初始状态一样,实际运行出来却是相同的重复过程,你需要人工设定一个保证随机性的初始状态。
I.I. 设置初始状态
设置随机数初始状态有三种语法形式:
1 | rand('seed', S) |
S是表示初始状态的整数。seed、state、twister就比较奇怪,令人捉摸不透,不知道该选用哪个。这实际上是产生随机数的不同算法。seed表示采用v4版本的随机数产生器,state是v5版本的随机数产生器,最后的twister用的则是Mersenne Twister随机数产生器。前两个随机数产生器都是“flawed”,推荐大家使用twister随机数产生器。
新版的Matlab默认采用Mersenne Twister随机数产生器,rng(S) 函数表示设定初始状态,rng('shuffle') 表示随机分配一个初始状态。所以现在只需要记住rng()函数设置初始状态,然后用rand产生随机数就可以了。
1 | rng(1); |
I.II. 产生非重复的随机数
2012版本之后的用户比较方便,在产生随机数之前使用rng('shuffle')洗一下就可以(shuffle是洗牌的意思)。
以前推荐的是rand('state',sum(100*clock))来根据当前时间设定初始状态,但时间始终是递增的,而且变化幅度相对来说很小,效果不是很好。有很多人用别的方式设定初始状态(如rand('twister', fix(mod(1e11*(sum(clock)-2009), 2^31)));),为简便起见,个人推荐采用新版Matlab中rng函数语法,即
1 | rand('twister',mod(floor(now*8640000),2^31-1)); |
II. 添加路径
1 | % 添加绝对路径, 并未添加其子文件夹 |
III. 数据集划分
划分数据集,产生训练集和测试集。
1 | % Split training-testing data |
IV. 矩阵除法求逆运算
如果要Moore-Penros广义逆的话可以用pinv(A); 如果只需要解方程Ax=b的一个解,可以直接x=A; 如果对精度要求比较高,不要用LU、QR,最好用SVD分解,根据需求来截断小奇异值。
inv:Y=inv(X)返回方阵X的逆矩阵,如果X病态或者高度奇异,则会显示警告信息。实际上,很少需要真的把矩阵的逆求出来,常见的使用失误主要出现在求解线性方程组AX=b。一种求解方法为x=inv(A)*b,但如要达到更快,更稳定,就得用X=A。这个算法使用高斯消去法,因此不产生逆矩阵。
如果A矩阵是非奇异方阵,则A,即inv(A)*B。而B/A是B乘A的逆矩阵,即B*inv(A)。具体计算时可不用逆矩阵而直接计算。使用符号“/”或“”会避免求逆,加速运算效率。换句话,(1/A)可以表示A的逆,这个算法使用高斯消去法,因此不产生逆矩阵。如果A矩阵不是方阵,可由以列为基准的Householder正交分解法分解,这种分解法可以解决在最小二乘法中的欠定方程或超定方程,结果是m×n的x矩阵。m是A矩阵的列数,n是B矩阵的列数。每个矩阵的列向量最多有k个非零元素,k 是A的有效秩。
“”:反斜线符号,矩阵左除。如果A是方阵,A(A)*B,只是他们的算法不一样。如果A是n*n的方阵,B是n*1的列向量,或n*?的矩阵,那么X=A=B的解。如果A很病态或者很奇异,很会显示警告信息。A(SIZE(A))计算A的逆,参见mldivide可得到更多信息。如果A是m*n的矩阵,m!=n,B是m*1或m*?的列向量,那么X=A=B(超定或者欠定)的最小二乘解。A的有效秩(effective rank)k有选主元的QR分解决定。Asolution X is computed that has at most k nonzero componentspercolumn。如果K<N,结果通常和
pinv(A)*B不一样,后者是最小范数解。A(SIZE(A))用来求解A的广义逆。
mldivide(A,B):等价于A,A和B必须有一样多的行,除非A是个标量(这时就等于.)。如果A是个方阵,A(A)*B,只是两者算法不一样。如果A是m*n的矩阵,那么X=A=B(超定或欠定)的最小二乘解,即(AX-B)的范数极小。
奇异矩阵求逆用pinv。经查证,inv是matlab的built-in函数。而pinv则可以看到其源码,不长,其实就是调用另外一个built-in函数SVD进行奇异值分解,再截断奇异值进行求解而已。所以pinv实际上就是截断奇异值求逆。
1 | 假定拟计算一般矩阵A的Moore-Penrose广义逆A+, |
奇异矩阵如何处理:奇异矩阵求逆,给矩阵主对角线每一个元素加一个很小的量,如1e-6;强制可逆。
V. PLOT设置
以下从一幅图可能涉及的多个方面进行罗列和演示:
1 | close all |
print()
用法:print(图形句柄,存储格式,文件名);
图形句柄,如果图形窗口标题栏是“Figure 3”,则句柄就是3.用gcf可以获取当前窗口句柄。
指定存储格式。常用的有:
png格式:'-dpng‘ (推荐这一种,与bmp格式一样清晰,文件也不大)
jpeg: ‘-djpeg‘(文件小,较清晰) tiff: ‘-dtiff‘
bmp: ‘-dbitmap‘(清晰,文件极大)
gif: ‘-dgif‘(文件小但不清晰)
文件名:自己给定
注意::print函数必须紧跟在plot函数之后使用。添加循环可以自动生成文件名。
V.I. 局部放大
- 将
magnify.m加载到 matlab 的安装路径中 - 运行程序,输出 figure
- 在 command window 中运行命令:
magnify - 在 figure 中编辑图形
- 按ctrl键,拖动鼠标左键,(也可以不按ctrl键,拖动鼠标右键)就可以放大局部图像了
- ctrl+左键固化,也可右键固化,‘<’和‘>’缩放方法范围(看细节-放大或者缩小细节)
- ‘+’和‘-’缩放放大比例 (确定需要放大的区域 ‘+’ 选取更大的区域,‘-’号,选取小区域)
- 在 figure 中编辑图形,使用 标记‘2’处的图形‘edit’或者使用Tools > Edit plot,鼠标选中目标如图中标记‘1’处的框,或者外面的放大区域。 进一步可以执行目标删除、放缩+上下左右移动等
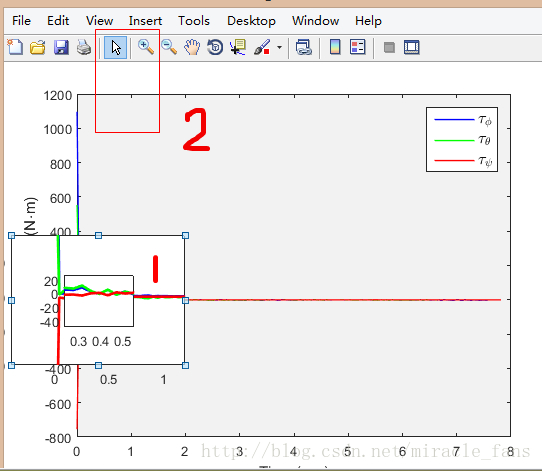
- 此时标记‘1’处的框已经被删除,上下左右调整放大框的位置,使用‘1’处的 insert 插入方框和箭头。
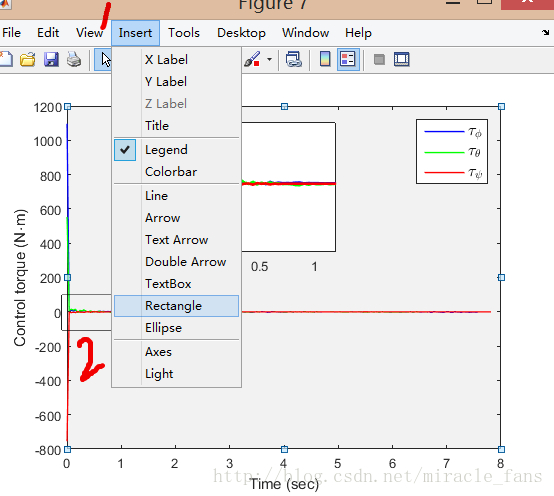
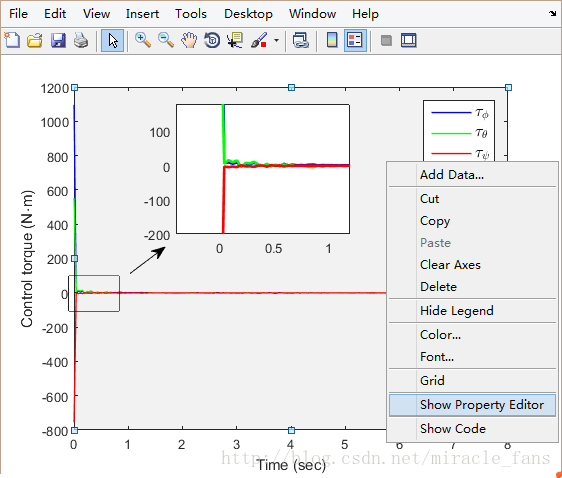
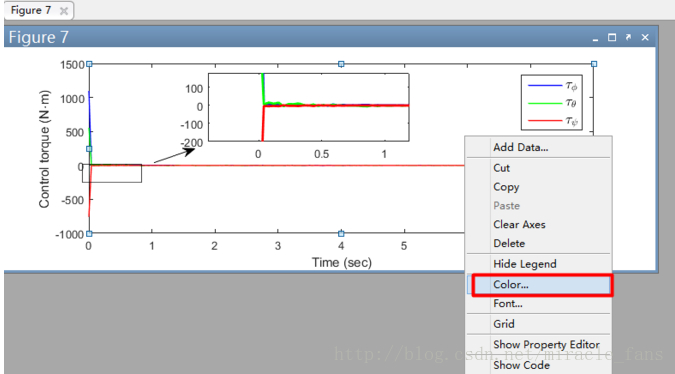
- 方框和箭头的位置,重回 edit 环境,在背景处右键-选择 show -property editor。选择‘white’在右面的三角号选择 ’ close ‘。或者如下图,使用背景-右键-color-white (方便快捷-推荐使用)。
VI. fill填充
对matlab中colormap的解释及fill、imshow的用法说明
VII. Legend控制
涉及到版本兼容问题,有些比较新的句柄属性在老版本Matlab中就用不起来,比如lineseries中的Annotation属性在我使用的R14SP1中就无法使用。
VII.I. Legend位置
LEGEND(...,'Location',LOC) 来指定图例标识框的位置
'North' 图例标识放在图顶端
'South' 图例标识放在图底端
'East' 图例标识放在图右方
'West' 图例标识放在图左方
'NorthEast' 图例标识放在图右上方(默认)
'NorthWest 图例标识放在图左上方
'SouthEast' 图例标识放在图右下角
'SouthWest' 图例标识放在图左下角
(以上几个都是将图例标识放在框图内)
'NorthOutside' 图例标识放在图框外侧上方
'SouthOutside' 图例标识放在图框外侧下方
'EastOutside' 图例标识放在图框外侧右方
'WestOutside' 图例标识放在图框外侧左方
'NorthEastOutside' 图例标识放在图框外侧右上方
'NorthWestOutside' 图例标识放在图框外侧左上方
'SouthEastOutside' 图例标识放在图框外侧右下方
'SouthWestOutside' 图例标识放在图框外侧左下方
(以上几个将图例标识放在框图外)
'Best' 图标标识放在图框内不与图冲突的最佳位置
'BestOutside' 图标标识放在图框外使用最小空间的最佳位置
利用位置属性进行精确设置
1 | gca=legend( 'sinx', 4 ); |
[0.1,0.1,0.9,0.9] 分别为axes在figure中的左边界,下边界,宽度,高度,最小为0,最大为1(左边界,下边界为0,上边界,右边界为1)
1 | figure |
VII.II. 图例说明m条 (m < n)
如果一个图中我们画了n条曲线,但是我们只想加图例说明(legend)的只有m条 (m < n)。例如你有25条曲线,想显示其中1,6,11,16,21的legend,则
VII.II.I. Annotation命令
1 | x = -3.14:0.1:3.14; |
EG. 1
2
3
4for i = [2:5 7:10 12:15 17:20 22:25]
set(get(get(H(i),'Annotation'),'LegendInformation'),'IconDisplayStyle','off');
end
legend('1','6','11','16','21');
VII.III. legend命令
把想要标注的图形命令给个变量名,然后再legend命令中指定。
1 | x = -3.14:0.1:3.14; |
EG. 1
2H = plot(data);
legend(H([1 6 11 16 21],'1,'6','11’,'16','21');
VII.IV. 多列legend
1 | t=0:pi/100:2*pi; |
只有第二个legend可拖动,而第一个legend不可拖动,原因不明。
VII.V. 避免legend覆盖曲线
给出的legend经常覆盖了某些曲线,这样就需要把legend分成几个,相对独立,这样可以使用鼠标随意移动,确保不遮挡曲线。
1 | a=linspace(0,2*pi,100); |
VII.VI. legend横排
1 | hl = legend(H([1 6 11 16 21],'1,'6','11’,'16','21'); |
VII.VII. legend不显示方框
1 | hl = legend(H([1 6 11 16 21],'1,'6','11’,'16','21'); |
VIII. errorbar
1 | ERRORBAR(X,Y,L,U),X是自变量,Y是因变量,L是Y的变动下限,U是Y的变动上限 |
IX. 柱状图
IX.I. 带有误差线(误差标记)的柱状图 errorbar
1 | % 生成示例数据 |


IX.II. 直方图的绘制
1 | %% 直方图图的绘制 |

IX.III. 柱状图的进阶
1 | %% =========柱状图的进阶========== |

IX.IV. 彩色柱状图
1 | %% 彩色柱状图 |

IX.V. 绘制统计直方图
1 | %% 绘制统计直方图 |

IX.VI. 均值方差直方图
1 | %% ========均值方差直方图======== |

IX.VII. 散点图
1 | %% =======散点图scatter , scatter3 , plotmatrix====== |
IX.VIII. 绘制区域图
1 | %% =========绘制区域图=========== |

IX.IX. 绘制饼状图
1 | %% =========绘制饼状图========= |

IX.X. 绘制填色多边形
1 | %% 绘制填色多边形。若每列的首尾元素不重合,则将默认把最后一点与第一点相连,强行使多边形封闭。 |

IX.XI. 绘制离散数据杆状图
1 | %% =======绘制离散数据杆状图=========== |

IX.XII. 绘制方向和速度矢量图
1 | %% =======绘制方向和速度矢量图======= |


IX.XIII. 轮廓线图的绘制
1 | %% ==========轮廓线图的绘制========== |

IX.XIV. Voronoi图和三角剖分
1 | %% ========= Voronoi图和三角剖分======== |

IX.XV. 三角网线和三角曲面图
1 | %% =========三角网线和三角曲面图======== |

IX.XVI. 彩带图ribbon
1 | %% ============彩带图ribbon======== |

IX.XVII. 在特殊坐标系中绘制特殊图形
1 | %% ==========在特殊坐标系中绘制特殊图形。======= |

IX.XVIII. 四维表现
1 | %% ======四维表现======== |

IX.XIX. 切片图和切片等位线图
1 | %% ======切片图和切片等位线图======= |
IX.XX. 动态图形
1 | %% =======动态图形========= |
IX.XXI. 影片动画
1 | %% =======影片动画 ======= |
X. MATLAB数据导出origin画图
数据导出: 1
save afile.txt -ascii a