优化算法系列

更新于 分类： 阅读次数： 本文字数： 1.6k 阅读时长 ≈ 6 分钟

优化技术是一种以数学为基础，用于求解各种工程问题优化解的应用技术。作为一个重要的科学分支，它一直受到人们的广泛重视，并在诸多工程领域得到迅速推广和应用，如系统控制、人工智能、模式识别、生产调度、VLSI技术和计算机工程等。

梯度为基础的传统优化算法具有较高的计算效率、较强的可靠性、比较成熟等优点，是一类最重要的、应用最广泛的优化算法。但是，传统的最优化方法在应用于复杂、困难的优化问题时有较大的局限性。一个优化问题称为是复杂的，通常是指具有下列特征之一：（1）目标函数没有明确解析表达；（2）目标函数虽有明确表达，但不可能恰好估值；（3）目标函数为多峰函数；（4）目标函数有多个，即多目标优化。一个优化问题称为是困难的，通常是指：目标函数或约束条件不连续、不可微、高度非线性，或者问题本身是困难的组合问题。传统优化方法往往要求目标函数是凸的、连续可微的，可行域是凸集等条件，而且处理非确定性信息的能力较差。这些弱点使传统优化方法在解决许多实际问题时受到了限制。

鉴于实际工程问题的复杂性、约束性、非线性、多极小、建模困难等特点，寻求一种适合于大规模并行且具有智能特征的算法已成为有关学科的一个主要研究目标和引人注目的研究方向。

最优化计算课程总结

I. 爬山算法

爬山算法是一种简单的贪心搜索算法，该算法每次从当前解的临近解空间中选择一个最优解作为当前解，直到达到一个局部最优解。爬山算法实现很简单，其主要缺点是会陷入局部最优解，而不一定能搜索到全局最优解。

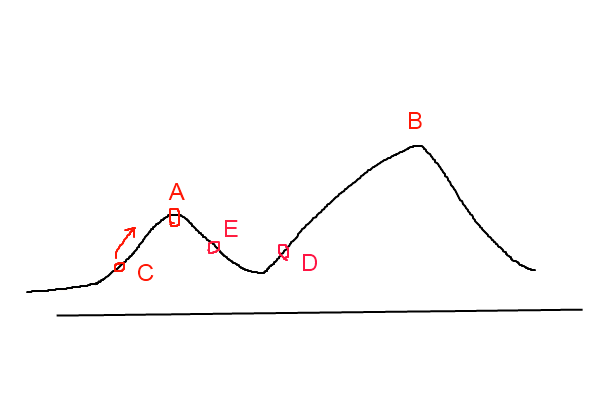
如图所示：假设C点为当前解，爬山算法搜索到A点这个局部最优解就会停止搜索，因为在A点无论向那个方向小幅度移动都不能得到更优的解。

II. 模拟退火

模拟退火1其实也是一种贪心算法，但是它的搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。

以上图为例，模拟退火算法在搜索到局部最优解A后，会以一定的概率接受到E的移动。也许经过几次这样的不是局部最优的移动后会到达D点，于是就跳出了局部最大值A。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/*
* J(y)：在状态y时的评价函数值
* Y(i)：表示当前状态
* Y(i+1)：表示新的状态
* r： 用于控制降温的快慢
* T： 系统的温度，系统初始应该要处于一个高温的状态
* T_min ：温度的下限，若温度T达到T_min，则停止搜索
*/
while( T > T_min )
{
　　dE = J( Y(i+1) ) - J( Y(i) ) ;

　　if ( dE >=0 ) //表达移动后得到更优解，则总是接受移动
Y(i+1) = Y(i) ; //接受从Y(i)到Y(i+1)的移动
　　else
　　{
// 函数exp( dE/T )的取值范围是(0,1) ，dE/T越大，则exp( dE/T )也
if ( exp( dE/T ) > random( 0 , 1 ) )
Y(i+1) = Y(i) ; //接受从Y(i)到Y(i+1)的移动
　　}
　　T = r * T ; //降温退火 ，0<r<1 。r越大，降温越慢；r越小，降温越快
　　/*
　　* 若r过大，则搜索到全局最优解的可能会较高，但搜索的过程也就较长。若r过小，则搜索的过程会很快，但最终可能会达到一个局部最优值
　　*/
　　i ++ ;
}

III. 遗传算法

遗传算法2是模拟生物在自然环境中优胜劣汰、适者生存的遗传和进化过程而形成的一种具有自适应能力的，全局性的概率搜索算法。遗传算法将问题的每一个可能性解看作是群体中的一个个体（染色体），并将每一个染色体编码成串的形式，再根据预定的目标函数对每个个体进行评价，给出一个适应值。算法将根据适应度值进行它的寻优过程。遗传算法的寻优过程是通过选择、杂交和变异三个遗传算子来具体实现的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
基本遗传算法伪代码

/*
* Pc：交叉发生的概率
* Pm：变异发生的概率
* M：种群规模
* G：终止进化的代数
* Tf：进化产生的任何一个个体的适应度函数超过Tf，则可以终止进化过程
*/
初始化Pm，Pc，M，G，Tf等参数。随机产生第一代种群Pop

do
{
　　计算种群Pop中每一个体的适应度F(i)。
　　初始化空种群newPop
　　do
　　{
　　　　根据适应度以比例选择算法从种群Pop中选出2个个体
　　　　if ( random ( 0 , 1 ) < Pc )
　　　　{
　　　　　　对2个个体按交叉概率Pc执行交叉操作
　　　　}
　　　　if ( random ( 0 , 1 ) < Pm )
　　　　{
　　　　　　对2个个体按变异概率Pm执行变异操作
　　　　}
将2个新个体加入种群newPop中
} until ( M个子代被创建 )
用newPop取代Pop
}until ( 任何染色体得分超过Tf， 或繁殖代数超过G )

优化遗传算法的性能：

  • 精英主义(Elitist Strategy)选择：是基本遗传算法的一种优化。为了防止进化过程中产生的最优解被交叉和变异所破坏，可以将每一代中的最优解原封不动的复制到下一代中。
  • 插入操作：可在3个基本操作的基础上增加一个插入操作。插入操作将染色体中的某个随机的片段移位到另一个随机的位置。

  1. 大白话解析模拟退火算法↩

  2. 遗传算法入门↩