Parameter Selection
模型的参数可分成两类:参数与超参数,前者是模型通过自身的训练学习得到的参数数据;后者则需要通过自身经验设置,以提高模型训练的效果。如神经网络中的隐层个数、每个隐层神经元个数、采用什么激活函数及学习算法、学习率以及正则化系数等都属于超参数。
一个模型的落地流程如下:
- 收集日志,并从日志中抽象出特征,再把特征喂给模型,模型在初始的超参数指导下学习第一类参数;
- 通过离线效果指标评估超参数的设定是否合适;
- 若不合适则继续不断调整。
在这个调参过程中主要有 2 个难点:
- 参数空间大,尝试成本高。在工业界往往数据规模巨大、模型复杂,计算成本很高,并且每个类型的超参数都有众多选择。
- 目标模型是黑盒。在搜索超参数的过程中只能看到模型的输入和输出,无法获取模型内部信息(如梯度等),亦无法直接对最优超参数组合建立目标函数进行优化。
I. 超参数选择方法
业界常用的搜索超参数方法主要有网格搜索、随机搜索和贝叶斯优化。
I.I. 网格搜索
网格搜索(Grid Search)是指在所有候选的参数选择中,通过循环遍历尝试每一种可能性,表现最好的参数就是最终的结果。
举个例子,有两类超参数,每类超参数有 3 个待探索的值,对它们进行笛卡尔积后得到 9 个超参数组合,通过网格搜索使用每种组合来训练模型,并在验证集上挑选出最好的超参数。
网格搜索算法思路及实现方式都很简单,但经过笛卡尔积组合后会扩大搜索空间,并且在存在某种不重要的超参数的情况下,网格搜索会浪费大量的时间及空间做无用功,因此它只适用于超参数数量小的情况。
I.II. 随机搜索
针对网格搜索的不足,Bengio 等人提出了随机搜索(Random Search)方法1。随机搜索首先为每类超参数定义一个边缘分布,通常取均匀分布,然后在这些参数上采样进行搜索。
随机搜索虽然有随机因素导致搜索结果可能特别差,但是也可能效果特别好。总体来说效率比网格搜索更高,但是不保证一定能找到比较好的超参数。
I.III. 贝叶斯优化
举个简单的例子,假设关于模型最优超参数组合的函数是一维曲线,由于它是一个黑盒无法直到具体的函数形式,但是可以输入某些值并得到输出。我们随机尝试了 4 个超参数,并得到了对应的性能指标,如下图所示2。
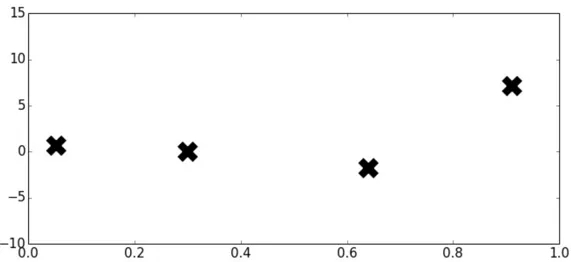
那么问题来了,最优超参数可能在哪里?下一个待探索的超参数是哪个?而每个人猜测的是不一样的,因此每次生成的函数也不同:
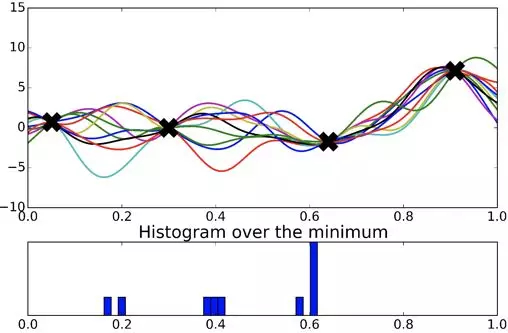

可以看到大部分都认为最优超参数是在第 3 个点附近, 由于开始时在右侧采点的离线指标是最差的,所以先验认为最优超参数在这里的可能性不大。接着把这个过程取极限,就会得到一个关于最优超参数的概率分布。假设每个分布都是高斯分布,那么得到的是一个高斯过程,其中高斯分布的均值为 0,方差大概为 5。
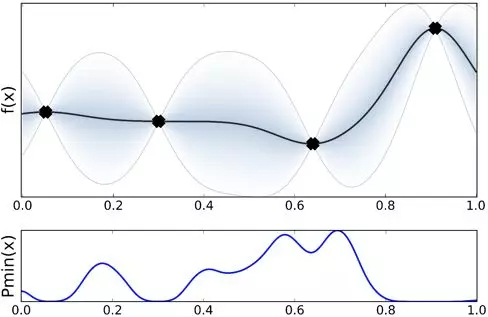
这样无论我们猜测最优超参数是取哪个值,总能得到一个关于超参数好坏的描述,即是均值和方差,这里实际上我们用一个无限维的高斯过程来模拟黑盒的超参数搜索的目标函数形式。
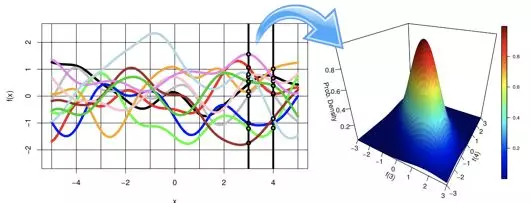
总结来说,超参数搜索问题其实是一个黑盒优化问题,贝叶斯优化通过无限维的高斯过程来描述黑盒,在这个高斯过程中可以得到每一组输入超参数的均值和方差。
得到了均值和方差则解决了上文提到的第一个问题:「最优超参数可能在哪里?」,那么下一个待探索的超参数是哪个?这其实是一个 E&E 问题(探索与利用问题),是稳妥地在目前已有的最大值附近搜索还是在不确定性大的地方搜索?后者效果可能很差,但也可能有意想不到的收获。而 Acquisition function 正是平衡 E&E 问题的方式。
- Upper (lower) Confidence Band 方法用线性加权的方式直接对 E&E 采样进行平衡,第一项是当前最好的超参数值,在当前最好的结果附近稳妥的搜索;第二项是方差,表示去探索更未知的空间,beta 参数用来控制力度,这种方法简单有效。
- Maximum Probability of Improvement 方法的目的是下一个待搜索的值能最大限度提升概率,假设当前最好的是 y_best, 那么 MPI 表示的是下一个待搜索的点能比 y_best 小的概率,这种方法容易陷入在局部最小值附近。
- Expected Improvement 描述的是下一个待搜索的点能比当前最好的值更好的期望,因为是高斯过程,这里的后验概率是高斯形式,积分有闭式解,实现起来较为简单,因此这种方法也较为常用。
可以看出贝叶斯优化(Bayesian Optimization)是通过 acquisition function 平衡均值和方差,做 E&E 问题探索下一个可能的最优超参数。
I.III.I. 实例1
如上方图所示,虚线代表关于最优超参数的真实函数形式(但实际上它是个黑盒,不知道其具体形式),实线代表当前最好的超参所在位置,两条浅灰线表示的是当前点的方差。
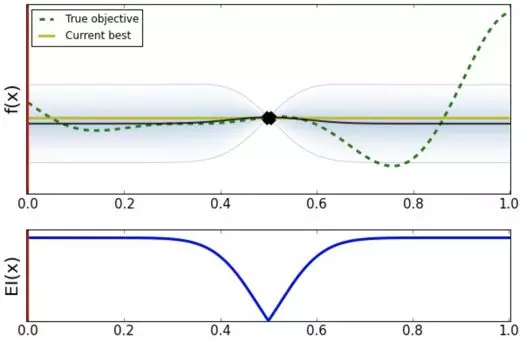
下方图表示已知的和待探索超参数的 Expected Improvement,此时很多地方都有希望能取得比当前最好值更好的超参数,主要需要探索,我们首先选择 0.0 点作为下一个待探索的超参数。
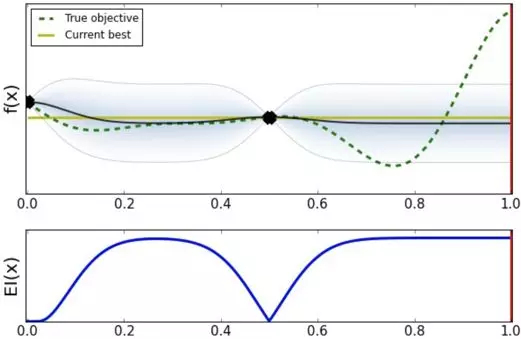
可以看到,此时 0.0 点的方差变为 0。继续寻找下一个待探索的超参数,选择 1.0。
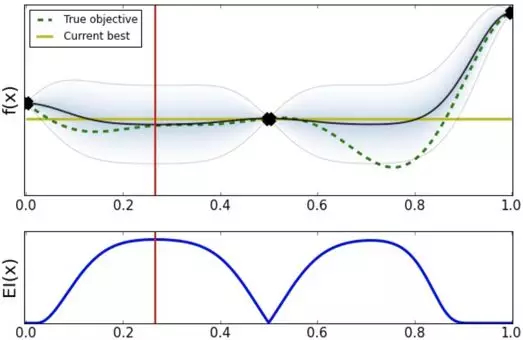
如图,1.0 点的方差变为 0,经过两次探索我们注意到不需要再探索右侧区域,因为我们在右边得到的超参数效果比左边的差。继续选择下一个超参数位置,选择 0.25 点左右的位置。
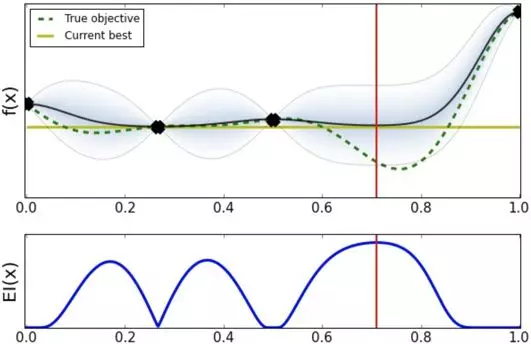
按照 EI 方法,依次寻找下一个待探索的超参数,这次我们选择的超参数位置大概在 0.7 点。
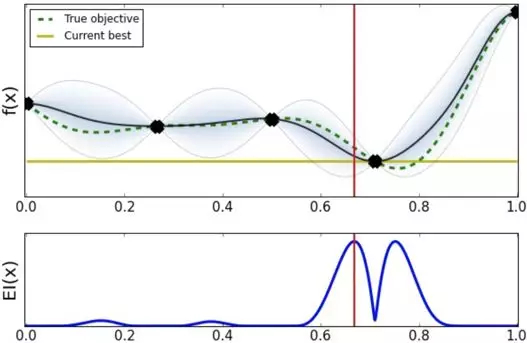
选择 0.7 点的超参数效果比之前选择的更好,此时 Expected Improvement acquision 建议应该加大在 0.7 附近搜索的力度。
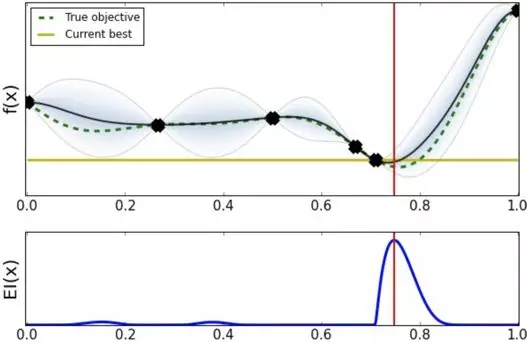
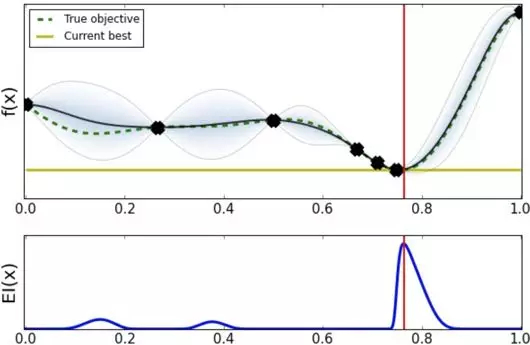
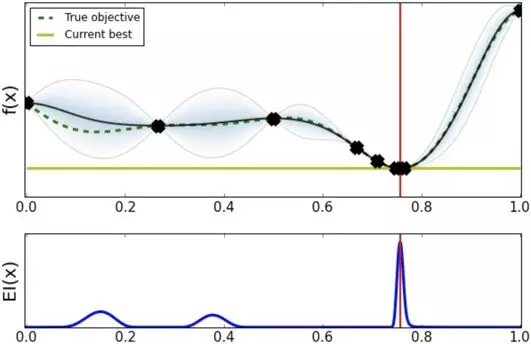
经过几轮探索之后发现最优超参数应该在 0.8 点附近。
II. SVM Parameter Selection
Support Vector Regression, which evolved from the support vector classification for doing regression tasks by introduction of the \(\varepsilon\)-insensitive loss function, is a data-driven machine learning methodology.
The parameter \(C\) controls the trade-off between the complexity of the function and the frequency in which errors are allowed. The parameter \(\sigma\) affects the mapping transformation of the input data to the feature space and controls the complexity of the model, thus, it is important to select suitable parameters, and the value of parameter \(\sigma\) should be selected more carefully than \(C\) .
Li, S., Fang, H. & Liu, X., 2018. Parameter optimization of support vector regression based on sine cosine algorithm. Expert Systems with Applications, 91, pp.63–77. Available at: http://dx.doi.org/10.1016/j.eswa.2017.08.038.
Li, S., Fang, H., 2017. A WOA-based algorithm for parameter optimization of support vector regression and its application to condition prognostics. 2017 36th Chinese Control Conference (CCC). Available at: http://dx.doi.org/10.23919/chicc.2017.8028516.
II.I. Metaheuristics
The matlab samples for svm parameter selection can be found in my Source repository.
To be continued...